Search
💪

강화학습 Week2(in progress)

생성일
2023/01/09 00:40
태그
강화학습
작성자

6.MDPs

6-1 Markov decision processes(MDPs)

MDPs의 전제는 환경이 fully observable하고,환경이 Markov Chain을 따른다는 것이다. 이는 환경이 다음의 식을 따른다는 것을 의미한다.
p(rt+1,st+1∣st,at)=p(rt+1,st+1∣Ht,at)p(r_{t+1},s_{t+1}|s_{t},a_{t})=p(r_{t+1},s_{t+1}|H_t,a_t)
첫 시점부터 t시점까지의 모든 히스토리를 몰라도 현재 상황만으로 미래의 상황을 알 수 있다는 의미이다. MDPs의 가정이 있어야 강화학습문제를 설정하고 풀기 용이하다. (또한 MDPs의 가정이 없다면 HtH_{t}를 이용해야 하므로 메모리 사용량이 매우 클 것이다)
지금까지 MDPs를 이용해서 강화학습을 푼다는 것의 광의를 살펴본 것이고, 이제부터는 이를 수학적 정의를 이용해서 알아보도록 하겠다.

6-2 MDPs의 요소(Componet)

•
𝒮 : 가능한 모든 상황들
•
A: 환경에서 에이전트가 행할 수 있는 모든 액션들
•
γ\gamma
◦
γ\gamma=0 은 행동 직후의 보상만 신경씀
◦
γ\gamma=1 은 시간 흐름에 따른 보상의 차이가 없음
•
𝑇: 전이확률
𝑇(s,a,s′)=p(s′∣s,a)𝑇(s,a,s') = p(s'|s,a)
s 환경에서 a 액션을 취했을 때 s’으로 넘어갈 확률
•
r : (𝒮 ,A) 를 인자로 가지는 보상함수으로, 기댓값의 형태를 가진다.
r=∑s′p(s′∣s,a)∗Rs′r=\sum_{s}^{'}p(s'|s,a)*R_{s'}
상황s에서 액션a를 취했을 때 한가지의 상황으로만 전이되지 않는다는 것을 이해하는 것이 핵심이다. 특정한 환경 s에서 특정한 액션a를 행했을때 발생가능한 상황들은 다양할 수 있다. 이를 상황 s′s'라고 표현한다. 이때 환경s에서 액션a를 행했을때 환경 s′s'으로 전이될 확률이 ∑s′p(s′∣s,a)\sum_{s}^{'}p(s'|s,a)이다. 또한 가능한 s′s'에 전이될때의 보상이 각각 존재하기 때문에 환경s에서 액션a를 취했을때의 보상은 기댓값으로 나타난다. 따라서 보상함수 r은 기댓값으로, ∑전이확률∗immediatereward\sum전이확률* immediate reward 으로 표현된다.
위에서 언급된 MDPs의 요소들을 예시를 통해 확인해보자
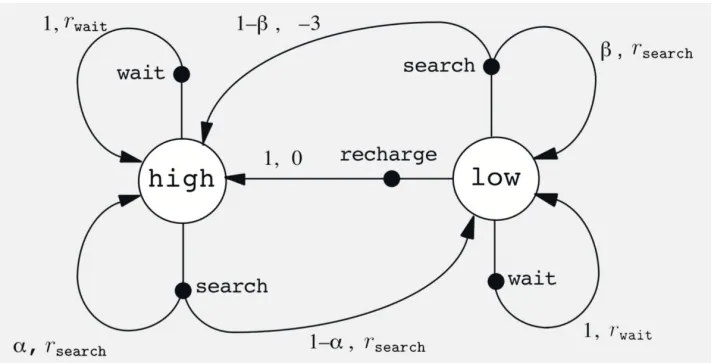
Example of MDP: Cleaning robot
•
S: {high, low}
•
A: high환경에서는 {wait,search}의 액션을, low환경에서는 {wait,search,recharge}액션을 행한다.
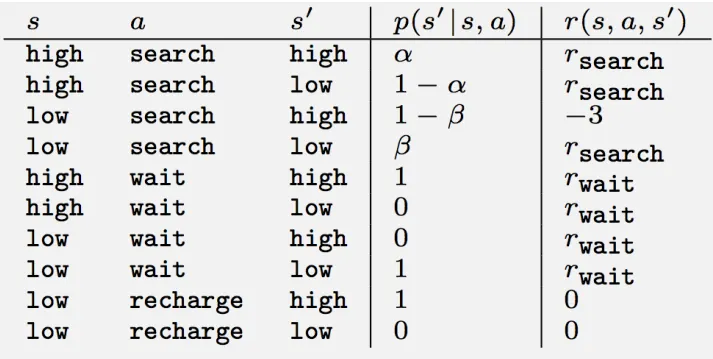
위에서 언급했듯이, 각각의 S에서 가능한 A를 행했을때 전이되는 환경 s′s'은 제각각이다. 이런 상황을 하나의 표로 나타낸것이 아래와 같다. 특정 s에서 가능한 액션a를 취했을때의 s′s'로 전이될 확률과 그때의 immediate reward를 하나의 표에서 확인할 수 있다.

6-3 learning in MDPs

그렇다면 이런 MDPs안에서 Reinforcement learning한다는 것은 정확히 어떤 의미인 것일까?
learning in MDPs=to Maximize Cumulative Rewardlearning\ in\ MDPs=to \ Maximize \ Cumulative \ Reward
이때 cumulative reward는 미래의 모든 보상들의 누적 합을 의미하고 이를 GtG_{t}으로 표현하고 return이라 말한다.
Gt=Rt+1+γRt+2+...=∑k=0∞γkRt+1+kG_{t}=R_{t+1}+\gamma R_{t+2}+...=\sum_{k=0}^\infin \gamma^kR_{t+1+k}
이때 discount(γ\gamma)를 사용하는 2가지 이유가 있다.
1.
Logical reason
때때로 immediate reward가 더 중요한 상황이 있을 수 있다. 이때는 γ\gamma의 값을 작게 해서 미래의 보상에 대해서는 값을 작게 한다.
2. Algorithmic/mathematical reason
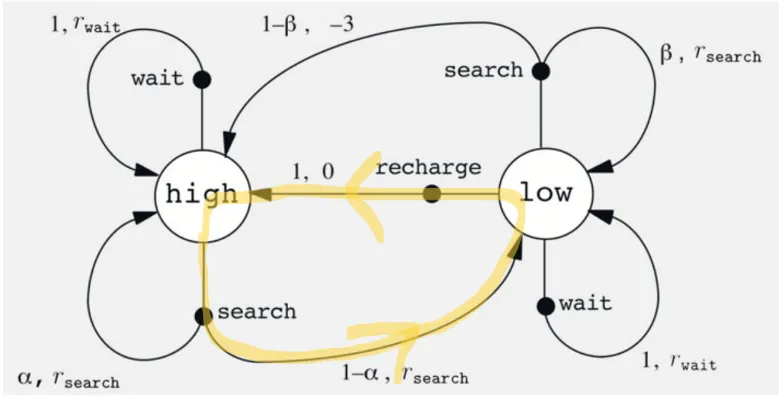
위와 같은 사이클을 반복할 수 있는 환경일 때 , 매 시점에서의 보상에 대해 discount을 하지 않는다면, GtG_{t}의 값을 무한대의 값을 가지게 되고, 이런 경우 올바른 학습을 할 수가 없기 때문에 discount를 해준다.
즉, 어떤 MDP에서 상태s에 따라 어떤 액션a를 선택해야 리턴의 값을 최대로 할 수 있는가 에 집중해야한다. 이를 정책 policy라고 한다.
특정 상태s에서 행할 액션a를 결정하는 policy는 π\pi라고 하고, 이를 확률로 나타내면 다음과 같다.
π(a∣s)=P[At=a∣St=s]\pi(a|s)=P[A_{t}=a| S_{t}=s]
위의 식처럼 정의되는 π\pi를 교정해나가며 더 큰 보상을 얻도록 하는 것이 강화 학습이다.
그렇다면, 위의 π\pi는 어떤 기준에 따라 정책을 수정해나가야 하는것일까? 이때 기준이 되는 것이 Value Functions 즉, return의 기댓값(estimate)이다. value functions에는 2가지가 있다.
1.
State value
vπ(s)=E[Gt∣St=s,π]v_{\pi}(s)=E[{G_{t}|S_{t}=s,\pi}]
상태s에서 정책 π\pi에 따를때 GtG_{t}의 기댓값으로 상태s의 밸류를 나타낸다. 그렇다면 vπ(s)v_{\pi}(s)의 확률변수는 무엇일까? 바로, 상태ss에서 행할 수 있는 액선a가 확률변수이다. 따라서 vπv_{\pi}는 다음과 같이 나타낼수 있다.
vπ(s)=∑aπ(s∣a)qπ(s,a)v_{\pi}(s)=\sum_{a}\pi(s|a)q_{\pi}(s,a)
2.
Action value
qπ(s,a)=E[Gt∣St=s,At=a]q_{\pi}(s,a)=E[{G_{t}|S_{t}=s,A_{t}=a}]
상태s에서 액션a를 취할때의 GtG_{t}의 기댓값으로, 액션a의 밸류를 나타낸다. qπ(s,a)q_{\pi}(s,a)의 확률변수는 상태 ss에서 액션 aa를 행했을때 전이될 수 있는 모든 상태 s′s'가 확률변수가 된다. 이를 확률과 확률변수의 곱으로 표현하는 것을 추후의 챕터에서 다룬다.
이 두가지 밸류를 보면 π\pi가 작은 글씨로 달려있는데, 두 값이 정책 π\pi에 따라 결정된다는 의미이다.
정리하자면, 특정 상황 ss 에서 value functions에 따라 π\pi를 수정해 나가면서