Search
💪🏼

Twin Delayed Deep Deterministic policy gradient (TD3)

생성일
2024/09/04 16:42
태그
강화학습
작성자

Introduction

•
Overestimation Bias
discrete action space에서 value estimates 가 overestimation되는 것을 의미한다.
일반적으로 Overestimation되는 오류는 Q-learning 에서 Value Function Approximation 할 때 발생하지만, Continuous space에서의 Actor-Critic 방법(DDPG) 에 대해서도 유사한 문제가 존재한다고 한다.
DDPG에서 봤듯이 noise가 있는 value function approximation은 (Crtic에서 Q-learning 과 같이 update 를 진행하면) overestimation이 발생할 수 있다.
또한, noise가 들어간다는 것은 아무튼 error가 계속해서 accumulate 되는 것이다 보니 agent가 optimal하지 않은 state나 action을 optimal 하다고 평가하게 되는 것이다.
이런 overestimation 문제를 해결하고자 Clipping Double Q-learning + Actor-Critic 형태로 변형하여 독립적으로 training 된 Critic 2개를 사용하였다고 한다. Overestimate된 value estimate 를 upper-bound 으로 사용하여, 실제 value estimates보다 낮은 estimates을 선호하도록 만들어 준다.
•
Variance reduction
Overestimation Bias를 줄이기 위해 Variance를 줄이는 몇가지 방법들
1.
Target network의 사용 - Accumulate error를 줄여 Variance를 줄이는 데 큰 도움이 된다. ( =DQN)
2.
delaying policy update - value estimation과 policy가 coupling (결합?) 되는 문제를 해결하기 위해 value estimation이 충분히 converge 될 때까지 policy update를 delay 시키겠다.
3.
Reularization strategy - SARSA처럼 similar action을 estimate하는 bootstrapping 방식을 적용하여 추가적으로 variance를 줄였다.

Background

•
Reinforcement Learning Objective
J(ϕ)=Esi∼pπ,ai∼π[R0]J(\phi) = \mathbb{E}_{s_i \sim p_{\pi}, a_i \sim \pi} [R_0]
강화학습의 목표는 parameter ϕ\phi 인 policy πϕ\pi_\phi 를 maximize하는 것이다. 즉, optimal policy πϕ\pi_\phi 는 expected return 인 J(ϕ)J(\phi) 를 maximize 해야한다.
∇ϕJ(ϕ)\nabla_{\phi} J(\phi)
update를 할 때는 expected return 의 gradient를 가지고 한다. 이 gradient는 policy의 parameter ϕ\phi 에 따르는 Return의 변화율을 의미하며 policy가 더 나은 방향으로 update된다.
•
Policy Gradient
∇ϕJ(ϕ)=Es∼pπ[∇aQπ(s,a)∣a=π(s)∇ϕπϕ(s)]\nabla_{\phi} J(\phi) = \mathbb{E}_{s \sim p_{\pi}} \left[ \nabla_a Q^{\pi}(s, a) \big|_{a=\pi(s)} \nabla_{\phi} \pi_{\phi}(s) \right]
TD3 는 DDPG에서 확장된 알고리즘이다보니 대부분 전개는 비슷하다.
Q-function Qπ(s,a)Q^\pi(s,a) : state ss 에서 action aa 를 취했을 떄 얻을 수 있는 value Policy gradient ∇ϕπϕ(s)\nabla_{\phi} \pi_\phi(s) : policy가 state ss 에서 선택하는 action 의 변화율
•
Q-learning
Q-learning 은 TD Method 방식으로 bellman equation 에 따라 update가 진행된다.
Qπ(s,a)=r+γEs′,a′[Qπ(s′,a′)],a′∼π(s′)Q^{\pi}(s, a) = r + \gamma \mathbb{E}_{s', a'} [Q^{\pi}(s', a')], \quad a' \sim \pi(s')
large state space에서 value는 parameter θ\theta 를 가진 function approximation Qθ(s,a)Q_{\theta}(s,a) 로 estimate 해 진행한다. ( =VFA)
y=r+γQθ′(s′,a′)y = r + \gamma Q_{\theta'}(s', a')
frozen target network Qθ′(s′,a′)Q_{\theta'}(s', a') 을 설정하고 objective 인 yy 를 update 한다.
•
soft target update
θ′←τθ+(1−τ)θ′\theta' \leftarrow \tau \theta + (1 - \tau) \theta'
TD3 도 stability 때문에 soft target update를 쓰는 것으로 보이고, DDPG와 살짝 다른점은 뒤에서도 다시 언급 하겠지만 Actor-Critic에서는 현재 사용중인 policy를 target policy로 사용하다 보니 Q-learning 처럼 update하려고 하면 target policy와 current policy 간의 차이가 거의 없어 일정 time steps 간격을 두고 (delay) update를 한다.

Overestimation Bias

Overestimation Bias in Q-learning

y=r+γmax⁡a′Q(s′,a′)y = r + \gamma \max_{a'} Q(s', a')
일반적인 Q-learning 에서 value estimates 는 greedy하게 update된다. 어떤 action이 사실은 optimal 하지 않더라도 max로 updatef를 하다보니 실제 값과 차이(error) 가 발생하게 된다.
Eϵ[max⁡a′(Q(s′,a′)+ϵ)]≥max⁡a′Q(s′,a′)\mathbb{E}_{\epsilon} \left[ \max_{a'} ( Q(s', a') + \epsilon ) \right] \geq \max_{a'} Q(s', a')
따라서 학습 초기에 error ϵ\epsilon 가 N(0,σ)\mathcal{N}(0,\sigma) 으로 시작하더라도 계속 update할 때 error가 accumulate 되다보면 결국엔 실제 value estimates 보다 더 커지게 될 것은 분명하다.

Overestimation Bias in Actor-Critic

Actor-Critic 에서는 policy가 Critic의 value estimate를 통해 update된다. DDPG의 연장선상이니까 Deterministic Policy Gradient 를 사용한다는 것을 base로 두고, Critic에서 update할 때, value estimate에서 왜 overestimation 이 발생하는지 증명하겠다.
ϕapprox=ϕ+αZ1Es∼pπ[∇ϕπϕ(s)∇aQθ(s,a)∣a=πϕ(s)]\phi_{\text{approx}} = \phi + \frac{\alpha}{Z_1} \mathbb{E}_{s \sim p_\pi} \left[ \nabla_{\phi} \pi_\phi(s) \nabla_a Q_{\theta}(s, a) \bigg|_{a = \pi_\phi(s)} \right]
ϕtrue=ϕ+αZ2Es∼pπ[∇ϕπϕ(s)∇aQπ(s,a)∣a=πϕ(s)]\phi_{\text{true}} = \phi + \frac{\alpha}{Z_2} \mathbb{E}_{s \sim p_\pi} \left[ \nabla_{\phi} \pi_\phi(s) \nabla_a Q^\pi(s, a) \bigg|_{a = \pi_\phi(s)} \right]
ϕapproxϕ_{approx} : 현재 policy의 parameter로, actor-critic 방법에서 approximate critic Qθ(s,a)Q_\theta(s, a)를 사용하여 업데이트된 parameter (=일반적으로 학습중인 policy)
ϕtrueϕ_{true} : true critic Qπ(s,a)Q^\pi(s, a) 에 의해 update된 hypothetical parameter
쉽게 설명하자면, ϕapprox\phi_{approx} 는 우리가 보통 환경에서 학습하는 동안 사용하는 건 approximate된 값이다. “approximate 했다는 건 결국 완벽하지 않다” 라고 볼 수 있고, 오차 (error) 가 존재할 수 있다는 것이다.
반대로 ϕtrue\phi_{true} 는 optimal policy로부터 update한 parameter인데, 사실 optimal policy라는건 실제 학습 중에는 알 수 없기 때문에 optimal policy가 이론적으로 존재한다고 가정해야하는 부분이 좀 있다.
where we assume Z1Z_1 and Z2Z_2 are chosen to normalize the gradient, i.e., such that Z−1∣∣E[⋅]∣∣=1Z^{-1}||E[·]||= 1
Z1Z_1과 Z2Z_2 는 gradient를 normalization하는 데 사용된다. 즉, 해당 expectation이 1이 되도록 하기 위한 scaling 상수이다. gradient 가 너무 커지거나 작아지는 것을 방지 하기 위해 쓴 것.
자, ϕapprox\phi_{approx} , ϕtrue\phi_{true} parameter를 사용하는 policy를 각각 πapprox\pi_{approx}, πtrue\pi_{true} 라고 해보자. 그러면 다음과 같은 3가지 조건이 반드시 성립한다.
1.
충분히 작은 ϵ1\epsilon_1 이 있을 때, learning rate α\alpha 가 ϵ1\epsilon_1 보다 작거나 같다면 ( ϵ1≥α \epsilon_1 \geq \alpha) , πapprox\pi_{approx} 의 approximate 된 값이 πtrue\pi_{true}의 approximate된 값보다 항상 크거나 같아야한다.
E[Qθ(s,πapprox(s))]≥E[Qθ(s,πtrue(s))]\mathbb{E} \left[ Q_{\theta}(s, \pi_{\text{approx}}(s)) \right] \geq \mathbb{E} \left[ Q_{\theta}(s, \pi_{\text{true}}(s)) \right]
→ 1번의 이유 : πapprox\pi_{approx} 는 approximate된 Critic QθQ_\theta 을 사용하여 update 되는 policy이다 보니, error (noise) 가 포함되었을 수 있음. 그렇기 때문에 πapprox\pi_{approx} 는 πtrue\pi_{true} 보다 크거나 같을 수밖에 없다.
2.
충분히 작은 ϵ2\epsilon_2 이 있을 때, learning rate α\alpha 가 ϵ2\epsilon_2 보다 작거나 같다면 ( ϵ2≥α\epsilon_2 \geq \alpha ), πtrue \pi_{true}의 실제 값은 πapprox\pi_{approx}의 실제 값보다 항상 크거나 같아야한다.
E[Qπ(s,πtrue(s))]≥E[Qπ(s,πapprox(s))]\mathbb{E} \left[ Q^\pi(s, \pi_{\text{true}}(s)) \right] \geq \mathbb{E} \left[ Q^\pi(s, \pi_{\text{approx}}(s)) \right]
→ 2번의 이유 : πtrue\pi_{true} 는 optimal한 value function QπQ^\pi 를 가지고 하기 때문에 optimal policy πtrue\pi_{true} 는 πapprox\pi_{approx} 보다 항상 좋아야한다.
3.
그리고, E[Qθ(s,πtrue(s))]≥E[Qπ(s,πtrue(s))]\mathbb{E} \left[ Q_\theta(s, \pi_{\text{true}}(s)) \right] \geq \mathbb{E} \left[ Q^\pi(s, \pi_{\text{true}}(s)) \right] 이 성립하고, 위의 2개의 수식에 대해 α<min⁡(ϵ1,ϵ2)\alpha < \min(\epsilon_1, \epsilon_2) 을 만족할 때 value estimation은 overestimate 되었다고 할 수 있다.
E[Qθ(s,πapprox(s))]≥E[Qπ(s,πapprox(s))]\mathbb{E} \left[ Q_\theta(s, \pi_{\text{approx}}(s)) \right] \geq \mathbb{E} \left[ Q^\pi(s, \pi_{\text{approx}}(s)) \right]
→ 3번의 이유 : approximate 된 policy πapprox\pi_{approx} 는 현재 학습 중인 approximate Q-funtion QθQ_\theta 를 가지고 action을 선택하므로 πapprox\pi_{approx} 가 선택한 action 도 QθQ_\theta 의 overestimate된 값에 기반하여 뽑게 된다. 따라서 πapprox\pi_{approx}에서도 overestimation이 될 것이다.
이렇게 overestimation 되는 이유는 DDPG에서는 Q-learning을 사용하는데 현재 Q-function에서 가장 높은 값을 뽑아버리기 때문. 만약에 Q-function이 overestimation 되어있다면 실제로는 좋지 않은 action에다가 높은 value를 주는 문제가 발생한다.
overestimation이 반복되면 지속적인 update에 의해 accumulate 되면서 bias가 심각하게 커져 부정확한 value estimation을 하게 될 것이고, 이는 poor policy update를 하게 되어 안좋은 policy가 되게 된다.

Clipped Double Q-Learning for Actor-Critic

기존에 여러 overestimation 문제를 줄이기 위한 방법들이 있었지만, actor-critic 구조에서는 효과적이지 않았다. 그래서 Double Q-learning의 변형인 Clipping Double Q-learning을 소개한다.
•
Learning target
강화 학습에서 "learning target"이란, 학습 과정에서 현재 policy를 update할 때 사용할 target value을 의미한다.
일반적인 Q-learning의 target은 다음과 같다.
y=r+γmax⁡a′Q(s′,a′)y = r + \gamma \max_{a'} Q(s', a')
rr은 현재 state에서 얻은 reward이고, γ\gamma는 discount factor, max⁡a′Q(s′,a′)\max_{a'} Q(s', a') 는 next state에서 취할 수 있는 action 중에서 가장 높은 Q-value를 선택해 target으로 설정하는 부분이다.
•
in Double DQN
Double Q-learning에서는 서로 다른 2개의 value estimator를 이용해 value function이 편향되지 않도록 만들어준다. 두 개의 Q-value가 서로 독립적이면, 한쪽 network가 overestimate 된 경우 다른 network가 이를 균형 맞추어 주는 방식으로 진행했다..
•
in Actor-Critic
Actor-Critic 에서는 Q-value가 아닌 policy를 직접적으로 학습한다. Actor는 policy를 업데이트하는 역할을 하고, Critic은 Q-value 또는 value function을 통해 Actor가 좋은 결정을 내릴 수 있도록 돕는 역할을 한다. 여기서 learning target은 Q-value 또는 value function을 기반으로 한다.
“learning target = Critic”
Actor-Critic에서는 Q-learning과 비슷한 접근을 하려 했을 때,  current policy과 target policy이 너무 비슷해서 독립적인 estimates를 만들기 어렵다. 따라서 2개의 Q-value를 사용하고 각 Q-value는 다른 Actor 에 맞춰서 학습하는 방식으로 진행된다.
y1=r+γQθ2(s′,πϕ1(s′))y2=r+γQθ1(s′,πϕ2(s′))y_1 = r + \gamma Q_{\theta_2}(s', \pi_{\phi_1}(s')) \\ y_2 = r + \gamma Q_{\theta_1}(s', \pi_{\phi_2}(s'))
즉, Qθ2Q_{\theta_2}는 πϕ1\pi_{\phi_1}로, Qθ1Q_{\theta_1} 는 πϕ2\pi_{\phi_2}로 학습하는 방식이다. 이렇게 함으로써 두 개의 독립적인 Q-value를 통해 Actor를 update하는 방식으로 구성되어있다. 서로 다른 Critic를 사용하여 두 actor가 교차로 들어가 optimize되는 구조로, 이는 unbiased value estimate를 가능하게 만들었다.
그런데? 문제가 있다.
Actor-Critic 구조에서 Double DQN 을 적용해도 여전히 DDPG와 유사한 overestimation 문제가 발생하고 있다. 물론 Double Q-learning을 써서 DDPG에 비해 overestimation을 줄이긴 했지만 완전히 제거하지 못하였다.
해당 이유는 두 Critic은 완전하게 independent 하지 않기 때문이다.
2개의 Critic Qθ1,Qθ2Q_{\theta_1}, Q_{\theta_2}이 learning target을 만들 때 반대편의 critic을 사용하고, 같은 replay buffer로 뽑히기 때문이다.
이로 인해 어떤 state s에서는 Qθ2(s,πϕ1(s))>Qθ1(s,πϕ1(s))Q_{\theta_2}(s, \pi_{\phi_1}(s)) > Q_{\theta_1}(s, \pi_{\phi_1}(s)) 일 수 있다. 일반적으로 Qθ1(s,πϕ1(s))Q_{\theta_1}(s, \pi_{\phi_1}(s)) 는 실제 value보다 overestimation 될 수도, 특정 부분에서는 훨씬 심하게 나타났다.
이러한 문제를 해결하기 위해 덜 biased 된 Qθ2Q_{θ_2}를 더 biased된 Qθ1Q_{θ_1}로 upper-bound으로 설정하여 제한 하였다.
다시 말하면 Qθ1Q_{θ_1} 가 일반적으로 더 편향되어있기 때문에, 보통은 Qθ2Q_{θ_2}이 더 true value (실제 값)에 가깝다고 생각할 수 있다. 그러나 만약에 Qθ2Q_{θ_2} 조차 편향되어 잘못된 값을 줄 수 있는 경우에 대비하여, 두 값을 비교하여 더 작은 값을 선택하겠다 라는 의미이다.
y=r+γmin⁡i=1,2Qθi′(s′,πϕ1(s′))y = r + \gamma \min_{i=1,2} Q'_{\theta_i}(s', \pi_{\phi_1}(s'))
결국 2개의 Critic 의 estimates 중에서 더 작은 값을 사용하여 (Clipping하여) learning target으로 사용한다.위와 같이 Clipping을 하면 Overestimation이 추가로 악화되지는 않는다.
반대로 이렇게 계속해서 target을 만드는 데 있어서 min을 사용하게 되면 underestimation 될 수 있다는 점도 생각해봐야한다. (poicy의 value를 실제보다 낮게 평가하는 것) 위 논문에서는 underestimated action 은 policy update를 통해 적극적으로 반영되어 update 되지 않으므로, 잘못된 action 이 좋다고 계속 유지되는 건 아니기 때문에 장기적으로 더 좋은 결과를 줄 수 있다고 말한다.

Reduced computation cost (using Single Actor)

이 부분은 읽어도 안읽어도 알고리즘 진행에 있어서 딱히 크게 문제 되지는 않지만 추가적으로 계산 비용을 줄인 방법을 소개한다.
위에서 Clipping Double Q-learning을 쓰면서 2개의 Actor와 2개의 Critic을 사용하였는데, Actor를 1개로 줄여보겠다는 것이다.
그 말인 즉슨, Critic Qθ1Q_{\theta_1}와 Qθ2Q_{\theta_2} 모두 동일한 target을 기반으로 update 하겠다는 것을 의미한다.
Actor를 1개로 줄였을 때, 달라지는 부분을 설명하자면
Qθ2>Qθ1Q_{θ_2} > Q_{θ_1}일 경우, Qθ1Q_{\theta_1}의 값이 true vale에 더 가깝거나, 적어도 overestimate 되지 않았다는 것 을 의미한다. 그래서 기존 Q-learning 처럼 Qθ1Q_{\theta_1}을 그대로 사용해도 문제가 없다. 이 경우, 추가적인 bias가 발생할 이유도 전혀 없다.
Qθ2<Qθ1Q_{θ_2}<Q_{θ_1}일 경우, Qθ1Q_{\theta_1}가 overestimated 되었을 가능성이 매우 높다고 볼 수 있다.
따라서, Double Q-learning 처럼, 더 작은 Qθ2Q_{\theta_2} 값을 선택하여 overestimate을 방지한다.
또한, function approximation error를 확률 변수 (random variable)로 두고, 이 random variable 집합에서 minimum을 선택하는 연산은 low-variance states 를 선호하게 된다.
이는 learning target이 low-variance value를 제공하는 state를 우선적으로 선택하게 되어 결과적으로 안정적인 policy update를 할 수 있도록 만들어준다.

Addressing Variance

앞에서 이야기 했던 내용이 결국 variance가 클 수록 overestimation의 가능성도 커진다는 것이다.
variance가 크면 학습 속도가 느려지고 실제 성능도 좋지 못하니까 학습과정에서 직접적으로 해결해야한다고 언급을 한다. 이제는 각 update에서 error를 minimize하는 것이 중요하다고 한다.
따라서, target networks and estimation error의 관계를 짓고, actor-critic의 variance reduction를 위한 학습 절차를 소개하도록 하겠다.

Accumulating Error

앞에서 했던 내용을 다시 정리하면, TD update 방식은 미래 state에 대한 estimates 를 기반으로 현재 state 의 value function를 update한다. 즉, 현재 state의 estimates가 다음 state의 estimates로부터 계산된다.
이 과정에서 한, 두번의 update로는 작은 error만 발생할 수 있겠만, 이러한 작은 error들이 반복되어 update되면 accumulate 된다. 이는 overestimation bias 가 발생할 가능성도 같이 증가한다.
function approximation 환경에서는 bellman equation을 정확히 만족시키기 어렵기 때문에 error 가 더욱 심각해질 수 있다.
Qθ(s,a)=r+γE[Qθ(s′,a′)]−δ(s,a).Q_{\theta}(s, a) = r + \gamma \mathbb{E}[Q_{\theta}(s', a')] - \delta(s, a).
각 update 후에도 일정한 양의 오차 δ(s,a)\delta(s, a) 가 남게 된다.
δ(s,a)\delta(s, a) 를 residual TD-error라고 부른다.
위의 수식을 전개해보면,
Qθ(st,at)=rt+γE[Qθ(st+1,at+1)]−δtQ_{\theta}(s_t, a_t) = r_t + \gamma \mathbb{E}[Q_{\theta}(s_{t+1}, a_{t+1})] - \delta_t
=rt+γE[rt+1+γE[Qθ(st+2,at+2)−δt+1]]−δt= r_t + \gamma \mathbb{E} \left[ r_{t+1} + \gamma \mathbb{E}[Q_{\theta}(s_{t+2}, a_{t+2}) - \delta_{t+1}] \right] - \delta_t
=Esi∼pπ,ai∼π[∑i=tTγi−t(ri−δi)].\\= \mathbb{E}_{s_i \sim p_{\pi}, a_i \sim \pi} \left[ \sum_{i=t}^{T} \gamma^{i-t}(r_i - \delta_i) \right].
이 과정이 반복되면서 최종적으로는 ( expected return - 미래의 TD-error의 expected discounted sum ) 형태로 나타나게 된다.
다시 말하면, value estimate는 미래에 얻을 reward와 error에 dependent 하다는 것이다. error가 accumulate 될수록 그 error의 variance도 커질 수 있다.
특히 discount factor γ\gamma 가 커질수록 각 update에서 error가 더 빠르게 accumulate 될 것이다. 그래서 error가 커지면 value estimates 의 variance도 크게 증가하게 되는 것이다.
추가로, minibatch 학습의 한계점도 언급을 하는데, 각 minibatch에서의 update는 전체 데이터에 대한 정보를 반영하지 않기 때문에, 각 minibatch에서의 gradient update는 error를 확실하게 줄일 수 있다는 보장이 없다

Target Networks and Delayed Policy Updates

•
Target Network의 필요성
target network가 없으면, 매번 update할 때마다 남아있는 residual error( δ(s,a)\delta(s, a) ) 가 축적될 수 있다. 즉, target network는 학습의 안정성을 높여, variance를 확실히 낮추는 역할을 한다고 볼 수 있다.
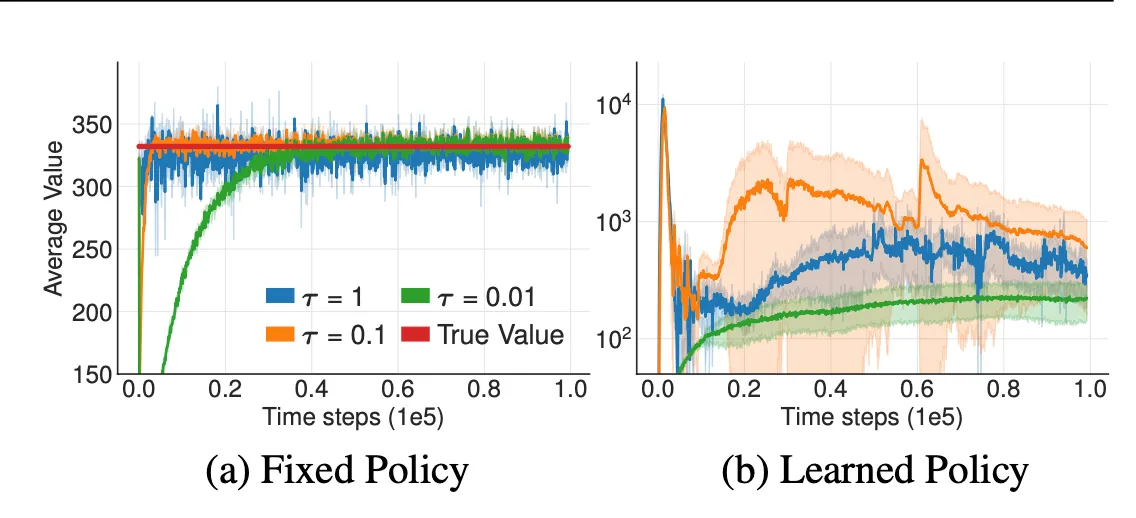
target network가 있는 경우 / 없는 경우로 비교한 결과 (target의 중요성)
target network 가 있는 (a) 의 경우 target network는 천천히 update된다. update 속도는 τ\tau 로 제어되며, τ\tau 가 클수록 update 속도는 빨라진다.
target network 가 있는 (b) 의 경우 value estimates를 update할 때 변동성이 매우 커진다. 즉, 학습 과정이 불안정하게 변한다.
fix된 policy에서는 update 속도와는 상관없이 결국에는 수렴하게 되지만, learnable policy를 쓰면 학습이 극단적으로 갈 수 있다.
•
Actor-Critic 방법이 학습이 실패하는 이유
일반적으로 actor-critc은 target network가 없는 on-policy이다. target network 없이 학습을 진행하면 policy update가 high variance 상태에서 이루어질 수 있다.
high variance 일떄 update를 하게되면 발산하는 action을 보일 수 있기 때문에 policy network 는 value network보다 낮은 빈도로 update를 해야한다. policy update를 value network의 error가 작아질 때까지 delay 시키는 것이다.
정확하게는 Critic은 매번 update를 하지만 policy network 와 target network는 일정 time step dd 이후에 update하도록 delay한다.
이렇게 했을 때 장점은 actor-critic에서 비슷한 critic에 대해 반복적으로 update하지 않으므로 low variance value estimates 를 사용할 수 있게 되고, 결과적으로 더 좋은 policy update를 할 수 있다.

Target Policy Smoothing Regularization

deterministic policy를 사용할 때, value estimate가 narrow peaks에서 overestimate 될 가능성이 높다.
peak : value estimates가 특정 state나 action 에 높은 value을 주는 것
특히 Critic을 update 할 때, deterministic policy를 사용하게 되면 function approximation error에 민감하게 반응한다. 이로 인해 value estimates의 variance가 증가하고, 학습이 불안정해질 수 있다.
이러한 문제를 해결하기 위해 Regularization 을 적용한다.
이 기법은 SARSA 에서 비슷한 action 은 비슷한 value를 가져야한다는 개념을 사용한다.
y=r+Eϵ[Qθ(s′,πϕ′(s′)+ϵ)]y = r + \mathbb{E}_{\epsilon} \left[ Q_{\theta}(s', \pi_{\phi'}(s') + \epsilon) \right]
target action의 주변에 비슷한 value estimate를 형성하도록 model을 fitting시켜주면 variance를 제거해줄 수 있을 것이다.
다시 말하면, target action에 작은 random noise를 추가하여 유사한 action 들이 유사한 value를 갖도록 만들어준다.
y=r+γQθ(s′,πϕ′(s′)+ϵ)ϵ∼clip(N(0,σ),−c,c)y = r + \gamma Q_{\theta}(s', \pi_{\phi'}(s') + \epsilon) \\ \epsilon \sim \text{clip}(\mathcal{N}(0, \sigma), -c, c)
실제로는 expectation 그대로 쓰지 않고, target policy에 random noise를 추가하고 mini-batch에서 평균을 내는 방식으로 진행한다.
random noise ϵ\epsilon 는 N\mathcal{N}(0,σ)(0,σ) 에서 sampling되어 clipping되어 target action이 원래 action에서 크게 벗어나지 않도록 만들어 준다.

TD3 Pseudo code