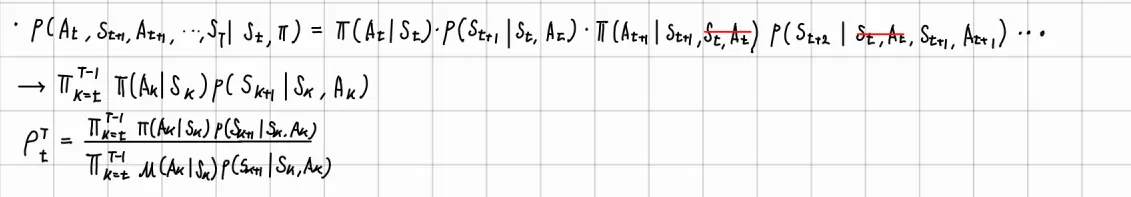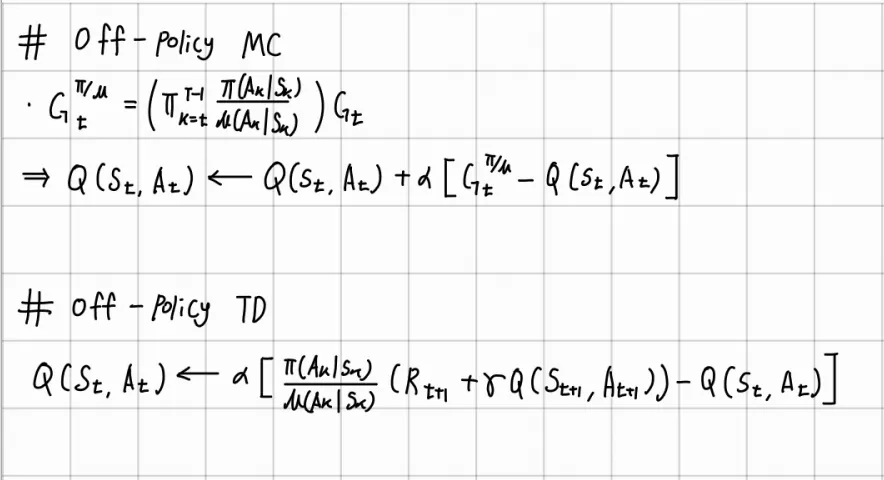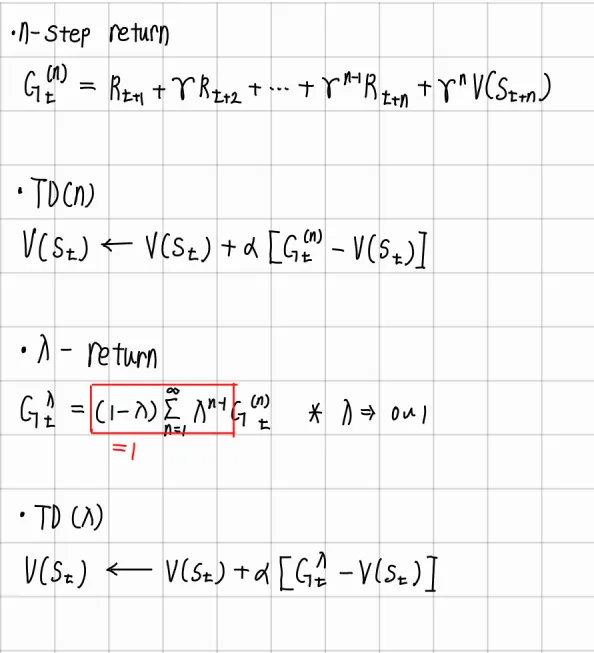Search
💪🏻

Temporal Difference

생성일
2024/07/16 06:17
태그
강화학습
작성자

1. Temporal Differnce 개요

•
Model-free, tabular updating 방식에 적용
•
TD Policy iteration
◦
Sampling episode에서 1-step transition을 기반으로 GPI를 적용
•
TD는 Bootstrapping 방식을 사용
◦
State-action value를 다음 state에서 계산한 추정량를 통해 update
◦
MC와 다르게 final outcome이 산출될 때까지 기다릴 필요가 없음

2. On-policy/Off-policy

•
Target policy와 behavior policy가 일치하는 것을 On-policy
•
Target policy와 behavior policy가 일치하지 않는 것을 Off-policy
•
Target policy는 target에서 action을 선택할 때 쓰는 policy
•
Target은 agent가 학습하려고 하는 목표
•
Behavior policy는 agent가 환경에서 action을 선택할 때 쓰는 policy
•
On-policy에서는 Policy improvement가 진행되고 나면 과거의 데이터를 사용할 수 없으나 Off-policy에서는 가능
◦
SARSA에서 target Q를 계산하는데 있어 이전 policy에서 얻은 (S′,A′)(S', A')은 현재 policy에서 유효한 값이 아니므로 사용 불가 (On-policy)
◦
Q-learning에서 target은 해당 state에서 가능한 action 중 Q-value를 최대로 만드는 값이므로 현재 policy와 무관하여 이전에 생성한 값 사용 가능 (Off-policy)
•
Off-policy에서는 behavior policy와 target policy가 다르기 때문에 exploration이 적용되어 전반적인 optimal을 향해 학습
•
On-policy에서는 suboptimal policy를 학습하게 될 위험이 있다.

3. SARSA

•
On-policy TD prediction
◦
Q(S,A)←Q(S,A)+α[R+γQ(S′,A′)−Q(S,A)]Q(S,A) ← Q(S, A) + \alpha [R + \gamma Q(S', A') -Q(S,A) ]
▪
Q(S,A)Q(S, A) update에 Q(S′,A′)Q(S' , A')가 사용되었으므로 bootstrapping
▪
1-step transition인 (S,A,R,S′,A′)(S,A,R,S',A') 을 바탕으로 update가 진행(TD 방식)
▪
Target policy와 behavior policy가 Q에 대한 ϵ−greedy\epsilon -greedy policy로 동일(On policy)
▪
QπQ^\pi를 target으로 하여 학습이 진행되기 때문에 Bellman expectation equation 사용

4. Q-learning

•
Off-policy TD prediction
◦
Q(S,A)←Q(S,A)+α[R+γmax⁡aQ(S′,a)−Q(S,A)]Q(S,A) ← Q(S, A) + \alpha [R + \gamma \displaystyle\max_a Q(S', a) -Q(S,A) ]
▪
Q(S,A)Q(S, A) update에 Q(S′,a)Q(S' , a)가 사용되었으므로 bootstrapping
▪
1-step transition인 (S,A,R,S′)(S,A,R,S') 을 바탕으로 update가 진행 (TD 방식)
▪
Target policy는 Q에 대한 greedygreedy, behavior policy는 Q에 대한 ϵ−greedy\epsilon -greedy (Off policy)
▪
Q∗Q^*를 target으로 하여 학습이 진행되기 때문에 Bellman optimality equation 사용
▪
직접 Optimal Q-function을 학습하기 때문에 성능 우수

5. Importance Sampling

•
MC, SARSA에서 off-policy의 장점을 활용하기 위해 behavior policy를 교체 가능
◦
Importance Sampling
▪
E[f]E[f]를 sample mean을 사용하여 추정한다고 가정
▪
Sampling 과정이 까다로울 경우 더 쉬운 분포에서 sampling 진행
▪
importance weights를 통해 보정
•
On policy 방식을 off policy로 변형 가능
◦
SARSA, MC의 behavior policy
▪
qπ(s,a)=Eπ[Gt∣St=s,At=a]q_\pi(s,a)=E_\pi[G_t|S_t=s, A_t=a]를 사용
◦
Return은 전체 trajectory의 확률을 따라 계산됨
◦
Behavior policy 교체
▪
GtG_t가 다른 distribution에서 추출되는 것
▪
다른 policy를 μ\mu라고 가정하면, importance weights는 아래와 같이 계산됨.
▪
원래 policy에서 trajectory의 확률새로운 policy에서 trajectory의 확률\frac{원래 \ policy 에서 \ trajectory의 \ 확률}{새로운 \ policy 에서 \ trajectory의 \ 확률}
▪
p(Sk+1∣Sk,Ak)p(S_{k+1}|S_k, A_k) 약분, transition probability를 모르더라도 weights 계산 가능
▪
따라서 policy의 교체가 model-free에서 가능
◦
Off policy의 장점을 on policy의 behavior policy 교체를 통해 활용 가능
▪
MC: behavior policy μ\mu에 의하여 experience를 쌓고 그것을 바탕으로 GtG_t를 계산하기 때문에 GtG_t에 weights를 곱해주어야 함
▪
TD : 1-step transition에서 behavior policy μ\mu를 사용하기 때문에 target에 weights를 곱해주어야 함(Tatget은 기존을 유지하고자 함)
•
단점
◦
MC : Target의variance가 증가로(확률값이 계속 곱해지므로) 수렴 속도가 느려질 수 있음
◦
TD : MC에 비해 variance의 증가가 적은 편

6. Bias vs Variance

•
Bias
◦
추정량들의 평균이 실제 값으로부터 얼마나 떨어져 있는가?
◦
작을수록 수렴이 빠름
◦
MC Target Return은 qπ(St,At)q_\pi(S_t, A_t)의 biased estimator
◦
TD target Rt+1+γQ(St+1,At+1)R_{t+1}+\gamma Q(S_{t+1}, A_{t+1})은 biased estimate이다.
•
Variance
◦
추정량의 기댓값이 그들의 중심으로부터 퍼져있는 정도
◦
작을수록 수렴 속도가 빠름
◦
TD target은 MC의 return과 비교했을 때 variance가 낮다
▪
Return이 많은 random 과정에 의해 결정되기 때문
•
일반적으로 MC는 Variance가 높고 TD는 bias가 높다.

7. MC, TD 정리

•
MC,TD 공통점
◦
Model free 상황에서 sample을 기반으로 직접 학습하는 방식
•
MC
◦
Return을 target으로 사용
◦
Episode의 마지막까지 기다려야 하며 반드시 종료되는 환경에서만 사용 가능
◦
Markov property에 대해 적은 영향을 받기 때문에 non-markov environments에서 효과적
◦
초기값에 강건
◦
Return이 불편추정량이므로 bias가 낮음
•
TD
◦
최종 결과까지 기다리지 않고 update하기 때문에 메모리 사용 측면에서 효율적
◦
Continuning environmet에서도 잘 작동
◦
Markov property 가정에서 자유롭지 못함
◦
초기값에 민감
◦
불편추정량을 target으로 사용하지 않기 때문에 bais가 높음
◦
Variance는 MC에 비해 낮은 편

8. Expected SARSA

•
기존 SARSA
◦
Next action을 선택 시 Q에 대한 ϵ−greedy\epsilon -greedy
•
Expected SARSA
◦
이 확률값들을 사용하여 action에 대한 기댓값을 적용한 target을 사용

9. Double Q-learning

•
Q-learning target에 maximization operation 포함
•
초기 단계에서 Q-value에 대한 overestimate가 발생
•
이것은 수렴 속도를 느리게 하는 문제가 있음
•
두개의 Q-function을 사용하여 문제를 해결
•
하나의 Q-table은 Target을 위한 Q-table이고 다른 하나는 maximization operation을 위한 Q-table이 됨.

10. TD(λ\lambda)

•
n-step return이란 현재 time step t에서 n-step만큼 진행하여 reward를 받고 n-step 이후에는 state value를 적용하여 return을 계산하는 방식
•
이때 n-step return을 target으로 사용하여 TD를 적용하는 것이 TD(n)
•
n-step return 여러개를 가중 평균 방식으로 합하여 Target으로 적용한 것이 TD(λ\lambda) 방식
◦
어떤 return 값을 더 중요하게 판단할 것인지에 대한 정보를 λ\lambda의 조정을 통해 추가할 수 있어 유용함
**TD(1)인 경우 Return으로 취급하여 MC 방식이 된다.

11. Examples

•
AB example
•
Answer
결과적으로 TD가 아직 생성되지 않은 future data까지 고려한다면 더 나은 성능을 보인다고 볼 수 있다. 왜냐하면 새로운 data를 더 생성한다면 75%의 비율만큼 reward를 1을 받는 data가 생성될 것이기 때문이다. 반면 MC는 기존에 존재하는 data에 충실한 답을 제공한다.
•
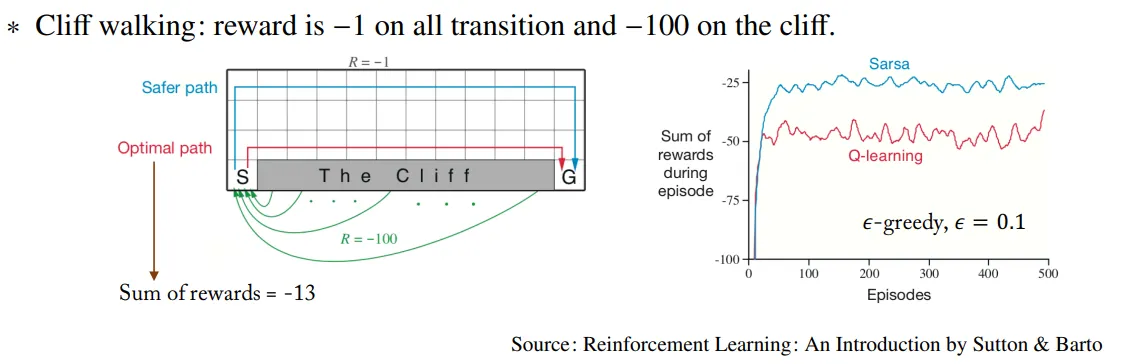
Cliff working
이 경우 Q-learning이 SARSA에 비해 성능이 낮게 나온다. 왜냐하면 SARSA의 경우 Target Policy와 behavior policy가 모두 Q에 대해 ϵ−greedy\epsilon -greedy policy이기 때문에, Cliff 근처에서 ϵ\epsilon만큼의 확률로 cliff로 빠지게 될 가능성을 고려하므로 항상 Q value를 Maximization 하는 방향으로 학습하는 Q-learning에 비해 안전한 경로를 선택하게 되고, 따라서 성능이 SARSA가 Q-learning이 ϵ\epsilon만큼 cliff에 빠지는 수치만큼 우수해진다.