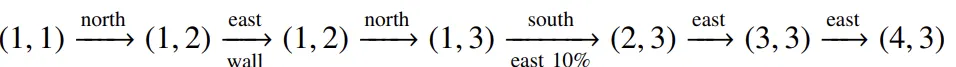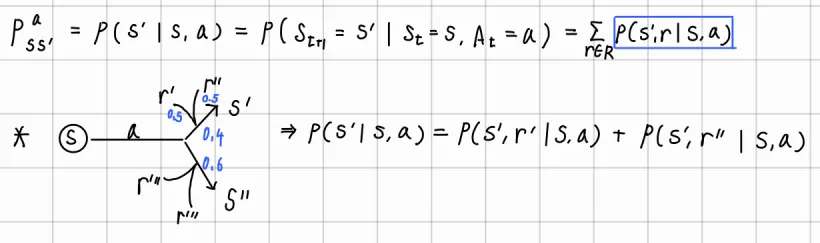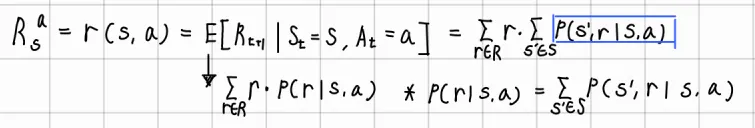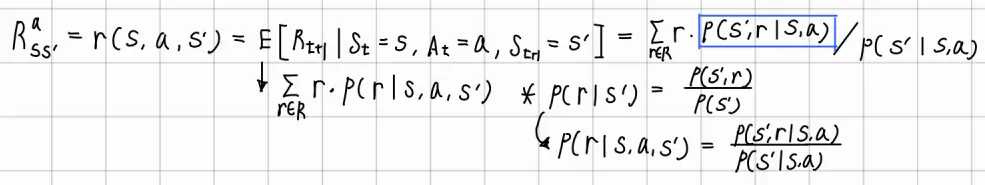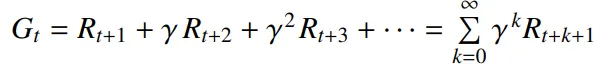💪🏻

MDP

생성일

2024/07/11 15:16

태그

강화학습

작성자

Markov Property

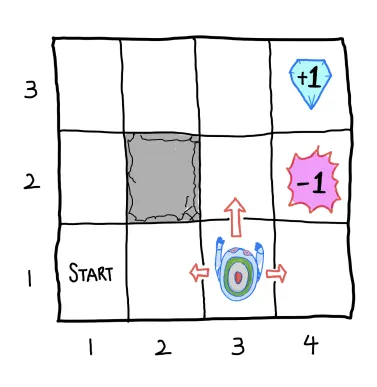
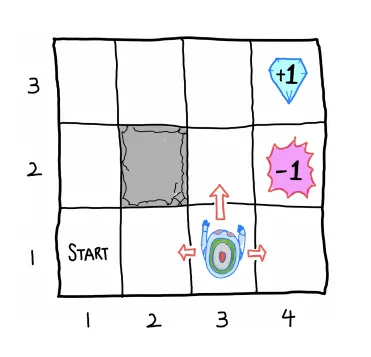
1. Grid world example

State :

S = \{(1,1), (1,2), ... , (4,2), (4,3)\}

Action:

A = \{north, south, east, west\}

Reward :

(4,3)

도달 시

+1

(4,2)

도달 시

-1

, Negative reward c (무의미한 이동 패널티)

Agent : Noisy movement

State trainsition probability

(2,2)(2,2)(2,2)에 도달 시 현재 상태 유지

선택한 방향 (80%)(80\%)(80%) , 좌/우 방향에 대해 10%10\%10% 확률로 이동 

Terminal state :

(4,2), (4,3)

Goal : Total sum of rewards를 maximize하는 policy 찾기

Episode

Total Reward : 5c+1

2. Actions in grid world

•

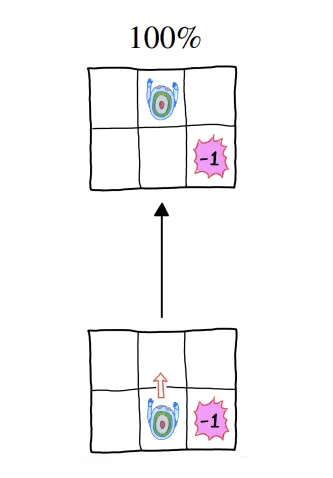
Deterministic

◦

Agent의 다음 state가 현재 state와 action에 의해서 완벽히 정해지는 경우

▪

 Policy가 정해지면 episode 1개만 가능

•

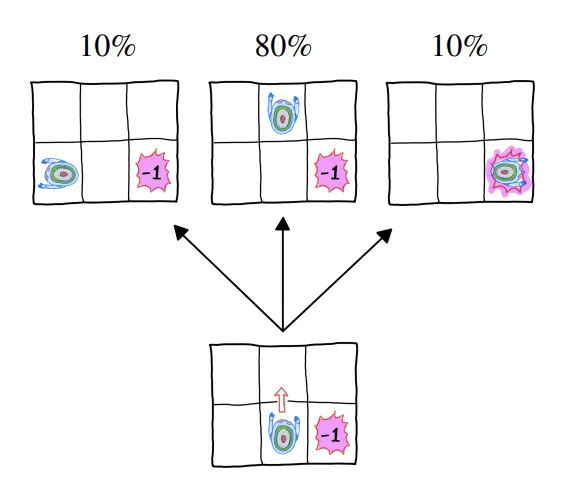
Stochastic

◦

Agent가 같은 state에서 같은 action을 하더라도 무작위성에 의해 다양한 결과가 가능

▪

Policy가 정해지더라도 여러 episode가 가능

3. Markov property

•

Stochastic Process

◦

시간에 따라 index가 부여된 확률 변수의 집합

◦

이산 확률 과정, 연속 확률 과정으로 구분

•

Markov Process

◦

확률 과정이 Markov property를 만족하면 Markov process라고 함

◦

 Markov property 만족?

▪

 현재 state  St=sS_t = sSt​=s 가 주어졌을 때 다음 state St+1=s′S_{t+1} = s'St+1​=s′ 이 될 확률이 과거의 상태들에 독립적이라는 것을 의미함. 

P(S_{t+1} = s'|S_t = s) = P(S_{t+1}=s'| S_0 = s_0 , ..., S_t=s)

•

State transition probability

◦

현재 state sss에서 다음 state s′s's′이 될 확률 (상태 전이 확률)

•

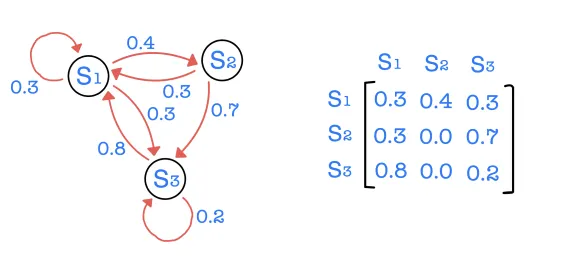
State transition probability matrix

•

Pij=Psisj=p(sj∣si)=P(St+1=sj∣St=si)P_{ij} = P_{s_is_j} = p(s_j|s_i) = P(S_{t+1}=s_j | S_t =s_i)Pij​=Psi​sj​​=p(sj​∣si​)=P(St+1​=sj​∣St​=si​) 

•

각각의 행의 합은 현재 상태에서 가능한 모든 미래 상태로의 진행 확률들의 합이므로 합은 1

결과적으로 Markov process는 (S, P)의 tuple 형태로 나타낼 수 있다. 이때 S는 state의 집합이고 P는 상태 전이 확률 행렬이 된다.

Markov Decision Process

1. MDP

•

MP

◦

 (State, Transition Probability)

•

MDP

◦

(action, reward, discount factor)

◦

모든 state는 Markov property를 만족

•

Transition Probability

◦

Pss′a=p(s′∣s,a)=P(st+1=s′∣St=s,At=a)P^a_{ss'} = p(s'|s,a)=P(s_{t+1}=s'|S_t=s, A_t=a)Pss′a​=p(s′∣s,a)=P(st+1​=s′∣St​=s,At​=a)

•

Reward function

◦

Action 선택의 기준

◦

Rss′aR^a_{ss'}Rss′a​ : 현재 state에서 action을 해서 다음 state로 전이될 때 얻게 되는 reward

◦

RsR_sRs​ : 현재 state에 존재하기만 하면 받게 되는 reward

◦

RsaR^a_sRsa​: 현재 state에서 action을 취했을 때 얻게 되는 reward

•

γ\gammaγ : 0~1 사이의 값으로 discount factor를 의미한다.

2. Environment model

•

MDP에서의 환경 모델

◦

전이 확률

◦

전이 확률을 아는 경우 ⇒ MDP를 안다 ⇒ Model-based ⇒ Dynamic programming ⇒ optimal policy

◦

전이 확률을 모르는 경우 ⇒ MDP를 모른다 ⇒ Model-free ⇒ Reinforce learning ⇒ optimal policy

3. Optimal policy in Grid world example

State :

S = \{(1,1), (1,2), ... , (4,2), (4,3)\}

Action:

A = \{north, south, east, west\}

Reward :

(4,3)

도달 시

+1

(4,2)

도달 시

-1

, Negative reward c (무의미한 이동 패널티)

Agent : Noisy movement

State trainsition probability

(2,2)(2,2)(2,2)에 도달 시 현재 상태 유지

선택한 방향 (80%)(80\%)(80%) , 좌/우 방향에 대해 10%10\%10% 확률로 이동 

Terminal state :

(4,2), (4,3)

Goal : Total sum of rewards를 maximize하는 policy 찾기

•

Optimal policy(π∗\pi_*π∗​)

◦

각 state에서 어떤 action을 선택할 것인지에 대한 정보

◦

위의 예시에서 9개 각각의 state마다 취하는 action을 결정하는 함수 = policy

▪

이때 state transition probability에 의해서 같은 action을 선택하더라도 전이되는 state가 다를 수 있음

▪

 그러므로 하나의 policy에 의해 여러 개의 episode가 생성될 수 있음.

▪

따라서 reward의 단순 합이 아닌 합의 기댓값을 최대화 하는 policy optimal policy π∗\pi_*π∗​로 나타냄

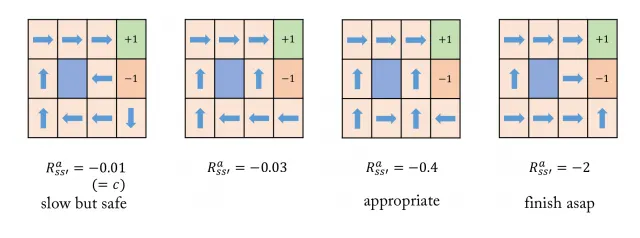
⇒ 위 그림은 각 모델마다 서로 다른 Optimal policy

•

Negative reward의 차이로 서로 다른 모델 = optimal policy 다름 

•

Small negative reward (c)(c)(c)의 값이 크면 각각의 이동에 대해 주어지는 Penalty가 작음

◦

 1번 case의 (3,2)에서 Optimal action이 west가 된다. 

▪

-1에 도달할 가능성을 완전히 배제하기 위한 것

▪

west action을 취하고 transition probability에 의해 north로 전이되기를 희망하는 것

▪

같은 이유로 (4,1)에서의 Optimal action도 south가 된다. 

◦

 2번 case에서는 c의 값이 1번에 비해 작아졌으므로, step의 증가에 따른 penalty가 늘어남

▪

 따라서 (3,2)와 (4,1)에서 optimal action이 달라짐.

◦

마지막으로 4번 case의 경우 각 step에 대한 penalty가 -2로 굉장히 큼 

▪

따라서 최대한 빠른 종료를 하도록 Optimal policy가 주어짐

▪

특히 (3,2)에서 east action을 optimal로 취급함

▪

만약 north action을 optimal로 취급하는 경우 가장 큰 reward는 -1인데, 이 경우는 -1을 얻기 위한 확률이 0.8*0.8=0.64가 되므로 (3,2)에서의 optimal action은 east임

Reward, Policy

1. Reward

•

Scalar feedback

•

t step에서 agent의 action이 얼마나 적절한지를 나타냄

⇒ agent의 목표는 reward의 누적 합을 최대화 하는 것

•

Reward Hypothesis

◦

강화학습의 모든 목표는 reward의 누적 합의 기댓값을 최대화 하는 것으로 표현 가능

◦

기댓값이 사용되는 이유는 하나의 policy를 따른다고 하더라도, transition probability에 의해서 나올 수 있는 episode가  다양하기 때문임.

2. Known dynamics

•

모든 transition에 대해서 dynamics( p(s′,r∣s,a)p(s',r|s,a)p(s′,r∣s,a) )를 안다고 가정하면 transition probability, reward 등을 이를 사용해 계산 가능

•

transition probability 

◦

현재 state sss에서 action aaa를 선택하여 다음 state s′s's′으로 전이하는 과정에서 얻을 수 있는 reward를 도입하여 transition probability를 표현할 수 있음(Marginalization)

•

Expected reward (state-action pair)

◦

기댓값 부분을 기댓값의 정의에 의해 표현.

◦

  p(r∣s,a)p(r|s,a)p(r∣s,a) 가 현재 state sss에서 action aaa를 선택했을 때 얻을 수 있는 reward에 대한 확률

▪

따라서 marginalization을 통해 state sss에서 action aaa를 선택했을 때 reward rrr을 받고 전이 가능한 모든 s′s's′에 대한 합으로 표현 가능

•

Expected reward (state-action-next_state)

◦

기댓값 부분을 기댓값 정의에 의해 표현. 

◦

 p(r∣s′)p(r|s')p(r∣s′)을 조건부 확률의 정의에 의해 표현 

◦

(s,a)(s,a)(s,a) 조건을 동시에 추가

⇒ 각 식의 전개 과정에 dynamics 항이 존재하므로, 이를 안다면 transition probability, reward는 dynamics를 통해 계산 가능하다.

3. Return

•

t 시점부터 종료 시점까지 감가된 reward의 누적 합이다. 

•

감가율 γ\gammaγ는 0~1 사이의 실수 값으로, 미래의 reward의 불확실성에 대한 표현

◦

 크기에 따라 근시안적이거나 원시안적인 모델임을 표현 가능

◦

 Discount factor를 사용하는 이유

▪

 return의 무한대 발산을 막음

▪

 미래의 불확실성에 대한 표현이 가능

▪

모든 sequence가 반드시 종료되는 경우 사용하지 않는 경우도 있음 

4. Policy

•

Stochastic policy

◦

주어진 state에서 취하는 action에 대한 확률 분포

◦

π(a∣s)=P(At=a∣St=s)\pi(a|s) = P(A_t=a | S_t=s)π(a∣s)=P(At​=a∣St​=s)

•

Deterministic policy

◦

π(s)=a\pi(s)=aπ(s)=a

Policy는 각 state에서 어떤 action을 취하는 것이 optimal한지, 즉 total discounted reward를 최대화하기 위한 action 선택에 대한 guideline이다. 이때 MDP에서의 policy는 MDP 각 state가 Markov property를 만족하기 때문에 오직 현재 state에 대해서만 종속적이다.

•

Case1) Known MDP

◦

 Deterministic optimal policy π∗(s)\pi_*(s)π∗​(s)가 존재한다.

•

Case2) Unknown MDP

◦

Stochastic policy를 고려해야 하며, ϵ−greedy\epsilon-greedyϵ−greedy 방식을 사용한다.

\epsilon-greedy

방식은

\epsilon

만큼 random한 action을 선택하고

1-\epsilon

만큼 greedy한 action(optimal)을 선택하여 현재 sample에서 비록 최적은 아닐지라도, 경험하지 않은 action에 대해서도 고려할 수 있도록 해준다. 이때

\epsilon

의 확률은 선택 가능한 모든 action에 대해서 동등하게 나누게 된다.

5. Notation

vπ(s)v_\pi(s)vπ​(s) : State-value function → 현재 state에서 policy π\piπ를 따랐을 때 가능한 모든 return에 대한 기댓값

v_*(s)

: Optimal state-value function → 현재 state에서 optimal policy

\pi

를 따랐을 때의 value

q_\pi(s,a)

: Action value function → 현재 state에서 action

a

를 선택하고 이후에

\pi

를 따를 때의 value

q_*(s,a)

: Optimal action-value function → 현재 state에서 action

a

를 선택하고 이후에

\pi_*

에 따를 때의 value

**이때 value는 각각 return의 기댓값을 의미한다.