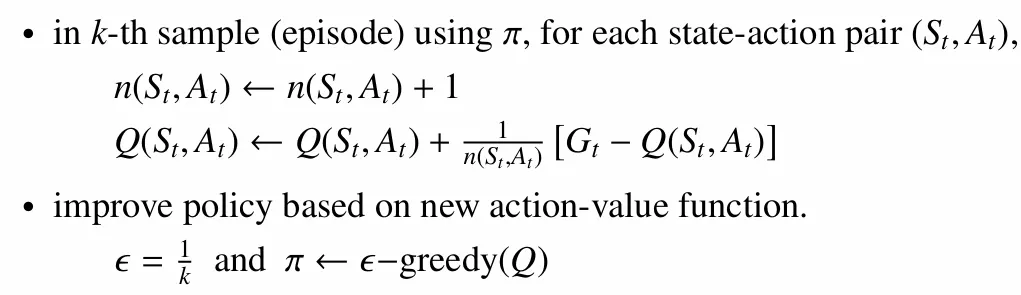Search
💪🏻

Monte Carlo method

생성일
2024/07/16 06:17
태그
강화학습
작성자

1. Monte Carlo method 개요

Monte Carlo는 random sampling을 반복하여 어떤 수치적 결과를 얻는 방법이다. 특히 Monte Carlo Policy iteration은 episode by episodic GPI 방식을 기반으로 하나의 episode에 대해 Policy evaluation과 Policy Improvement를 적용하는 것을 전체 episode에 대해 반복적으로 진행한다. 특히 PE에서 MC를 활용한 학습은 하나의 episode가 종료된 이후 그 episode의 전체 trajectory를 바탕으로 진행되며, 여기서 실제로 경험한 state에 대해서만 update를 진행하기 때문에 계산량이 줄어든다는 장점이 있다. 그리고 Value의 추정에 episode sample에서 얻은 Return의 평균을 사용하는데, 이것은 MC 방식이 bootstrapping을 사용하지 않는다는 것을 나타내고 따라서 Markov property 가정이 다소 위배되어도 영향이 적다는 것을 파악할 수 있다. 이때 bootstrapping 방식이란, 추정량의 update에 다른 추정량를 사용하여 update하는 것을 말하며, 만약 현재 state-action pair의 value를 Rt+1+γQ(St+1,At+1)R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})을 사용하여 update한다면 이는 bootstrapping이 될 것이다.여기서 알 수 있듯이 Q value update에 bootstrapping 방식을 적용한다면, 현재 state의 정보를 바탕으로 다음 state의 value가 정확히 계산되어야 하는데, 이를 가능하게 하려면 Markov property의 가정을 만족하는 것이 반드시 필요하다.

2. Monte Carlo Prediction

Monte Carlo Prediction ( Policy evaluation ) 에서의 목적은 주어진 Policy π\pi를 바탕으로 얻은 episode를 사용하여 정확한 qπq_\pi 값을 학습하는 것이다. 여기서 qπ(s,a)=Eπ[Gt∣St=s,At=a]q_\pi (s,a) = E_\pi[G_t| S_t = s, A_t = a ] 로 정의되는 qπq_\pi의 추정을 위해, 실제 return GtG_t의 기댓값을 계산하는 것이 아닌 empirical mean return을 사용한다. Empirical mean return를 사용한다는 것은, 각각의 episode sample에서 얻은 state-action pair에 대해 1n∑Gt\frac{1}{n}\sum G_t 를 계산하여 학습에 사용한다는 것이다. 추가로 하나의 episode 내에서는 동일한 state-action pair가 여러개 존재할 수 있는데, 알고리즘에 따라 처음 방문한 경우의 return만 고려하여 Empirical mean return에 반영할 수도 있고 모든 방문에 대해 고려할 수도 있다.
•
Estimate qπ(s,a)q_\pi (s,a) ( MC )
1.
increment count : n(s,a)←n(s,a)+1n(s,a) ← n(s,a) + 1
2.
increment total return : S(s,a)←S(s,a)+GtS(s,a) ← S(s,a) + G_t
3.
Q(s,a)=S(s,a)n(s,a)Q(s,a) = \frac{S(s,a)}{n(s,a)}
→ 각각의 episode에서 (s,a)(s,a)의 Return을 계산하여 방문 횟수로 나누어 평균 return을 구한다.
→ 만약 first visit MC라면 첫 방문 시의 return만 고려하고 Every visit인 경우 전체 방문 고려
→ 큰 수의 법칙에 의해 방문 횟수가 매우 커지면, 추정량는 실제 qπq_\pi에 수렴하게 된다.

3. Incremental Monte Carlo updates

Incremental mean을 사용하여 효율적으로 update를 진행하는 것이 가능하다.
Incremental mean : μk=μk−1+1k(xk−μk−1)\mu_k =\mu_{k-1} + \frac{1}{k}(x_k - \mu_{k-1})
•
Estimate qπ(s,a)q_\pi(s,a) ( Incremental mean + MC )
1.
increment count : n(s,a)←n(s,a)+1n(s,a) ← n(s,a) + 1
2.
Q(St,At)←Q(St,At)+1n(St,At)[Gt−Q(St,At)]Q(S_t, A_t) ← Q(S_t, A_t) + \frac{1}{n(S_t, A_t)}[G_t - Q(S_t, A_t)]
→ Incremental mean을 적용하지 않았을 때와 비교하였을 때 increment total return을 저장하기 위한 변수를 추가하지 않아도 된다는 장점이 있다.
→ n(St,At)n(S_t,A_t)의 값이 episode가 늘어날수록 작아지게 되므로 최근에 계산되는 return 값의 영향이 줄어들게 되는 단점이 있다.

4. Constant - α\alpha MC policy evaluation

Incremental MC에서 최근에 계산되는 return의 영향이 여러 episode에 대해 계산이 진행될수록 작아지는데 이는 비교적 최근에 계산된 값이 발전된 policy에 의해서 계산된 value이기 때문에 단점이 된다. 따라서 step-size α\alpha를 도입하여 이를 해결한다.
•
Estimate qπ(s,a)q_\pi(s,a) ( Constant- α\alpha + MC )
1.
Q(St,At)←Q(St,At)+α[Gt−Q(St,At)]Q(S_t, A_t) ← Q(S_t, A_t) + \alpha[G_t - Q(S_t, A_t)]
→ 과거 episode에서 계산된 Q(St,At)Q(S_t, A_t)가 지수적으로 영향이 감소한다.
→ 최근 정보에 대해 더 영향력을 부여한다.

5. Exploitation vs Exploration

•
Exploitation
: 가장 높은 Q-value를 가지는 action을 선택하는 것을 의미한다
•
Exploration
: Q-value와 관계없이 일정 확률로 다른 action을 선택하는 것을 의미한다.
→ 경험해보지 않은 action 중에서 best action이 존재할 수 있으므로 ϵ−greedy\epsilon -greedy 방식을 사용하여 exploitation과 exploration의 적절한 균형을 맞춰주어야 한다.

6. Monte Carlo Control (ϵ−greedy\epsilon -greedy Policy Improvement)

•
Dynamic Programming에서는 Model-Based이므로 Policy Improvement를 위해
π’(s)=arg max⁡aQπ(s,a)\pi’(s) = \displaystyle \argmax_a Q^\pi(s,a), 즉 deterministic policy를 사용한다.
•
MC Control은 Model-Free 상태에서 진행되기 때문에 일정 비율로 exploration을 위해
ϵ−greedy\epsilon -greedy Policy를 사용한다.
이때, Policy Improvement에서 ϵ−greedy\epsilon-greedy Policy를 사용하고자 한다면, Policy의 개선을 보장하기 위해 아래의 정리를 만족해야 하며 증명 과정은 아래 첨부 이미지와 같다.

7. GLIE MC control

→ 학습하는 Policy가 다음의 조건을 만족한다면 GLIE라고 부른다. 각 state-action pair에 대해서 무한히 많은 방문이 진행되었고, 무수히 많은 episode sample에 대해 학습 과정이 진행되었을 때 Policy가 greedy policy로 수렴해야 한다.
이를 바탕으로 GLIE MC control 문제를 다뤄보면, 1번 조건은 episode sample을 확대하는 것이 최선이다. 2번 조건의 경우 iteration의 증가에 따라 ϵ→0\epsilon → 0이 되도록 하는 방식을 고려한다. 따라서 이를 적용한 GLIE MC control은 아래와 같다.
→ K가 늘어날 때마다 ϵ\epsilon이 작아지게 되어 π\pi가 greedy policy로 수렴하게 되는 방식을 적용한다. 결과적으로 iteration이 진행됨에 따라 Q(s,a)→q∗(s,a)Q(s,a) → q_*(s,a)가 된다.

8. Monte Carlo Method 정리

(b)에서 Return의 평균을 사용하여 Q-value를 update하는 prediction이 진행되었고 (c)에서 (b)에서 계산한 Q-value를 바탕으로 Q-value를 최대화 하는 action과 나머지 action에 대한 선택 확률을 배정하여 ϵ−greedy\epsilon -greedy 방식으로 control을 진행하는 흐름이다.