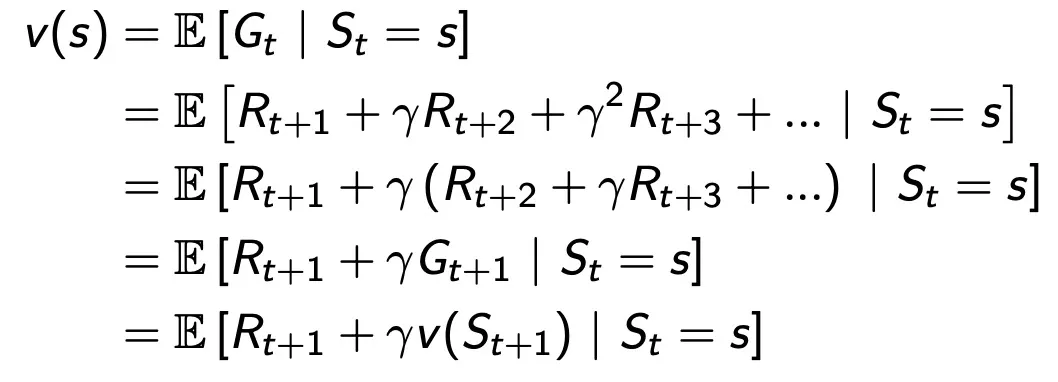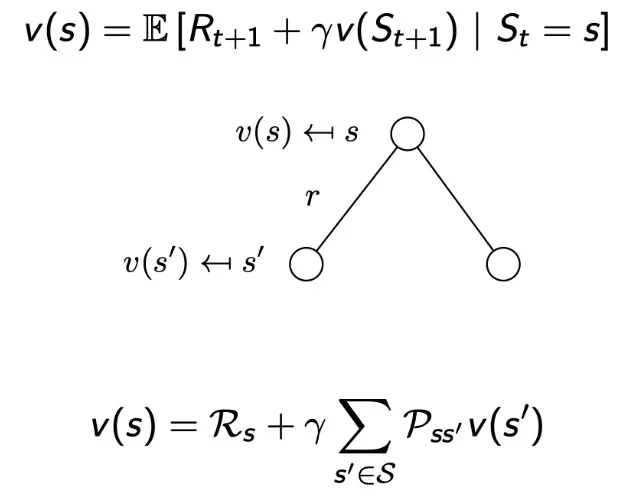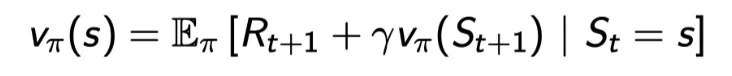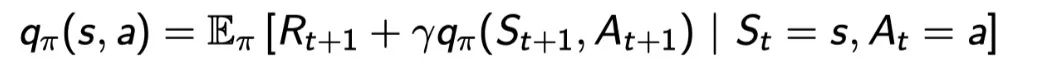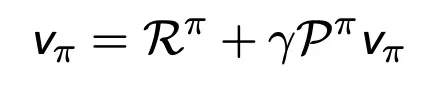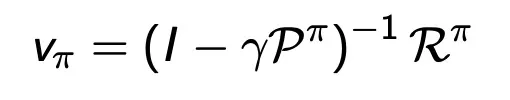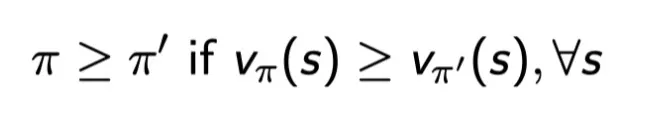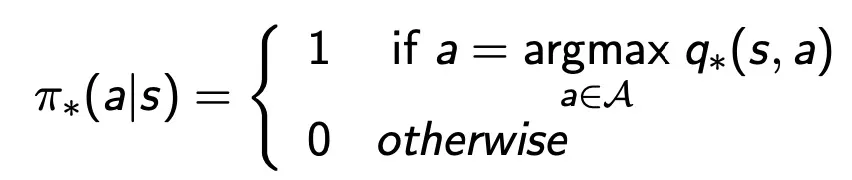🍏

2장

Introduction to MDPs

•

Markov decision processes formally describe an environment for reinforcement learning

•

Where the environment is fully observable

•

Almost all RL problems can be formalised as MDPs, e.g.

Markov Property

The state captures all relevant information from the history

Markov Process

A Markov process is a memoryless random process.

→ memoryless : 어디서 어떻게 왔든 상관없이 미래는 현재에서 결정한다는 뜻 (Markov Property)

a sequence of random states S1, S2, ... with the Markov property.

→ random process는 sampling을 할 수 있다는 의미. (Markov property를 가진 random state의 순서를 의미)

•

S : state들의 집합.

•

P : 다음 state로 전이할 확률.

Markov Reward Process

•

S : 스테이트들의 집합

•

P : 트랜지션 확률 매트릭스

•

R : 리워드 함수 (어떤 스테이트에 도착하면 어떤 리워드를 줘라.를 스테이트 별로 정의 해두는 것.)

•

γ : discount factor

Return

The discount γ ∈ [0, 1] is the present value of future rewards

γ close to 0 leads to ”myopic” evaluation γ close to 1 leads to ”far-sighted” evaluation

Why discount?

•

Mathematically convenient to discount rewards

•

Avoids infinite returns in cyclic Markov processes

•

It is sometimes possible to use undiscounted Markov reward processes (i.e. γ = 1), e.g. if all sequences terminate.

Value Function

return 의 기댓값. 어떤 state에 왔을 때, 계속 sampling 하면서 에피소드를 만들어간다.

그럴 때 에피소드마다 리턴이 생기게 된다.

Bellman Equation for MRPs

immediate reward R(t+1)

Markov Decision Processes (MDP)

•

A Markov decision process (MDP) is a Markov reward process with decisions. 

•

It is an environment in which all states are Markov.

Policies

•

A policy fully defines the behaviour of an agent

•

MDP policies depend on the current state (not the history)

Value Function

state-value function

•

input은 state 하나이다.

•

action이 따로 없었던 MRP와는 달리 action이 추가되면서 policy π가 추가됐다.

•

여전히 그 의미는 현재 스테이트 s에서 출발했을 때 얻을 수 있는 return의 기댓값을 의미한다.

action-value function

•

Q함수라고도 부른다. 

•

input은 state와 action 2개가 들어간다. 

•

state s에서 action a를 했을 때 그 이후에는 policy π를 따라서 게임을 끝까지 진행했을 때 return의 기댓값을 의미한다.

Bellman Expectation Equation

state-value function decompose

한 스텝을 가고, 그 다음 스테이트부터 pi를 따라가는 것과 같다.

action-value function decompose

R(t+1)을 받고, 다음 state에서 다음 액션을 하는 것의 기댓값들.

다음 액션은 pi에 의해 결정된다.

Bellman Expectation Equation (Matrix Form)

→ 역행렬을 통해서 direct solution을 구할 수 있다.

MDP가 커지면 계산량이 너무 커져버리는 단점이 있다.

Optimal Policy

“policy pi를 따랐을 때, 모든 state-value가 pi’ 을 따랐을 때보다 더 좋을 때 pi가 pi’ 와 같거나 뛰어나다” 라고 할수 있다.

단, 여기서 하나의 state-value라도 pi’ 것보다 좋다고 할 수는 없다.

Finding an Optimal Policy

An optimal policy can be found by maximising over q∗(s,a),

There is always a deterministic optimal policy for any MDP

If we know q∗(s,a), we immediately have the optimal policy

Solving the Bellman Optimality Equation

•

Bellman Optimality Equation is non-linear 

•

No closed form solution (in general)

Many iterative solution methods