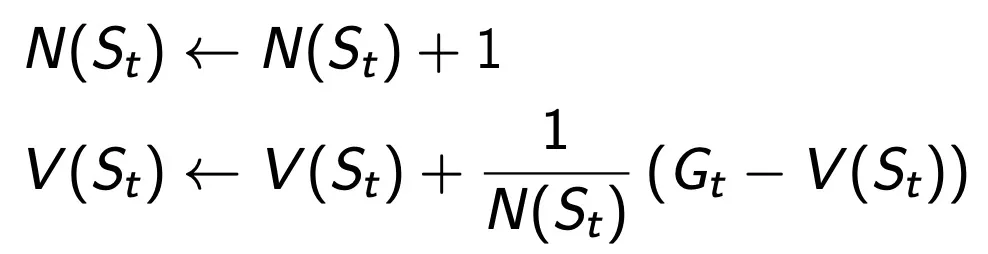🍏

4장

Monte-Carlo Reinforcement Learning

계속된 실행으로 도출한 실제 값들을 통해서 추정하는 방식

MC methods learn directly from episodes of experience

MC is model-free: no knowledge of MDP transitions / rewards

MC learns from complete episodes: no bootstrapping, 이 값들을 평균낸 것이 value

계속 loop한 episode의 경우 return 이 나오지 않으므로, episode는 종료되어야 한다.

First-Visit Monte-Carlo Policy Evaluation

The first time-step t that state s is visited in an episode, Increment counter N(s) ← N(s) + 1

Increment total return S(s) ← S(s) + Gt , Value is estimated by mean return V(s) = S(s)/N(s) → 대수의 법칙에 인해 n이 무한대로 가면 V(s)는 Vpi(s)로 수렴한다.

Every-Visit Monte-Carlo Policy Evaluation

Every time-step t that state s is visited in an episode, Increment counter N(s) ← N(s) + 1 Increment total return S(s) ← S(s) + Gt , Value is estimated by mean return V(s) = S(s)/N(s)

→ 모든 state를 방문한다는 가정하에, 대수 법칙에 따라 두 방식의 결과는 같다.

Incremental Monte-Carlo Update

V(s)를 방문할 때마다 Incremental Mean을 통해 update한다.

non-stationary에서는 1/N을 a와 같은 작은 값으로 고정하는 것이 좋을 수 도 있다.

→ 오래된 경험은 삭제시키고 1/N은 최신 기억이 쌓일 수록 update되는 것을 보정시켜서 최신값으로만 evaluate하게 만든다.

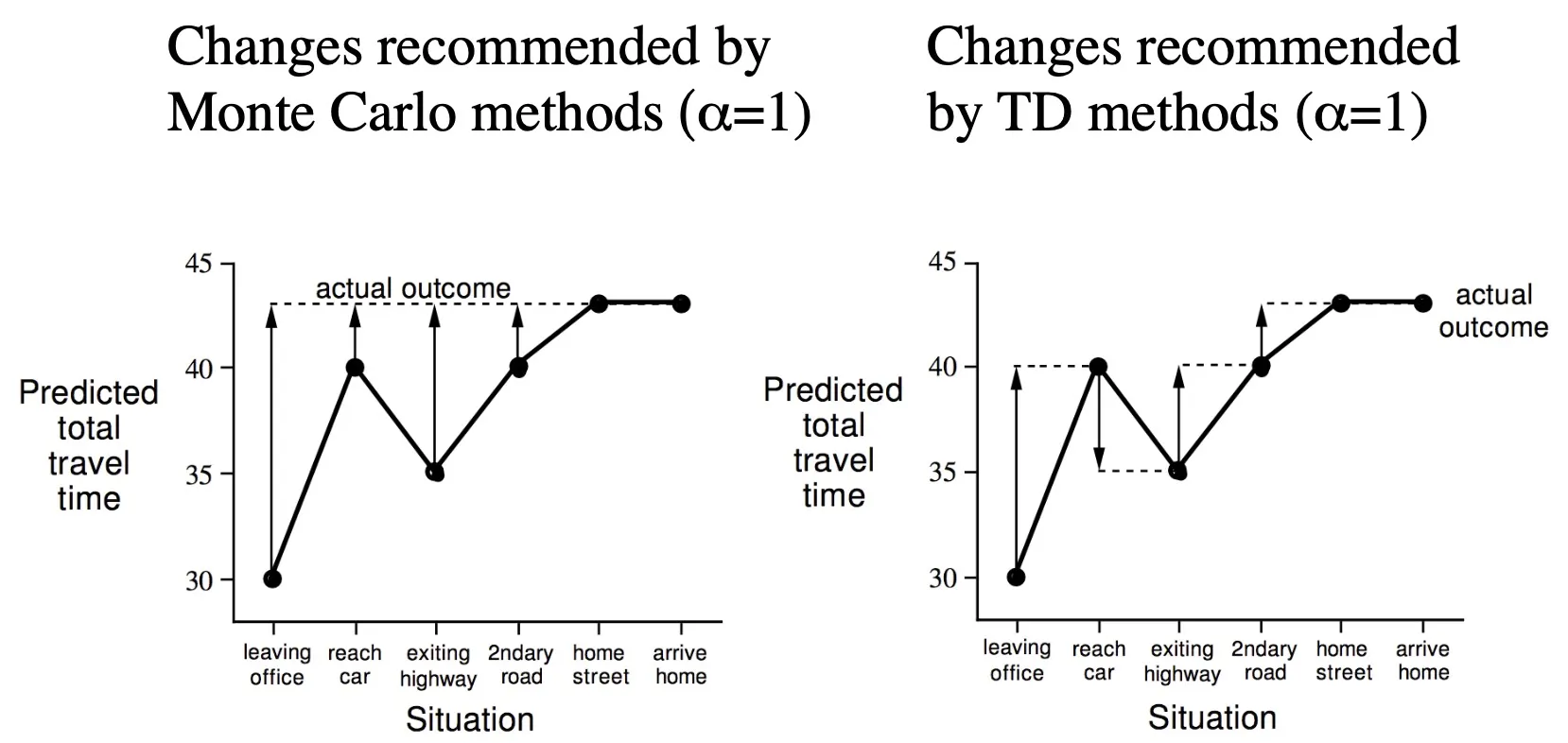
Temporal-Difference Learning

TD methods learn directly from episodes of experience

TD is model-free: no knowledge of MDP transitions / rewards

TD learns from incomplete episodes, by bootstrapping

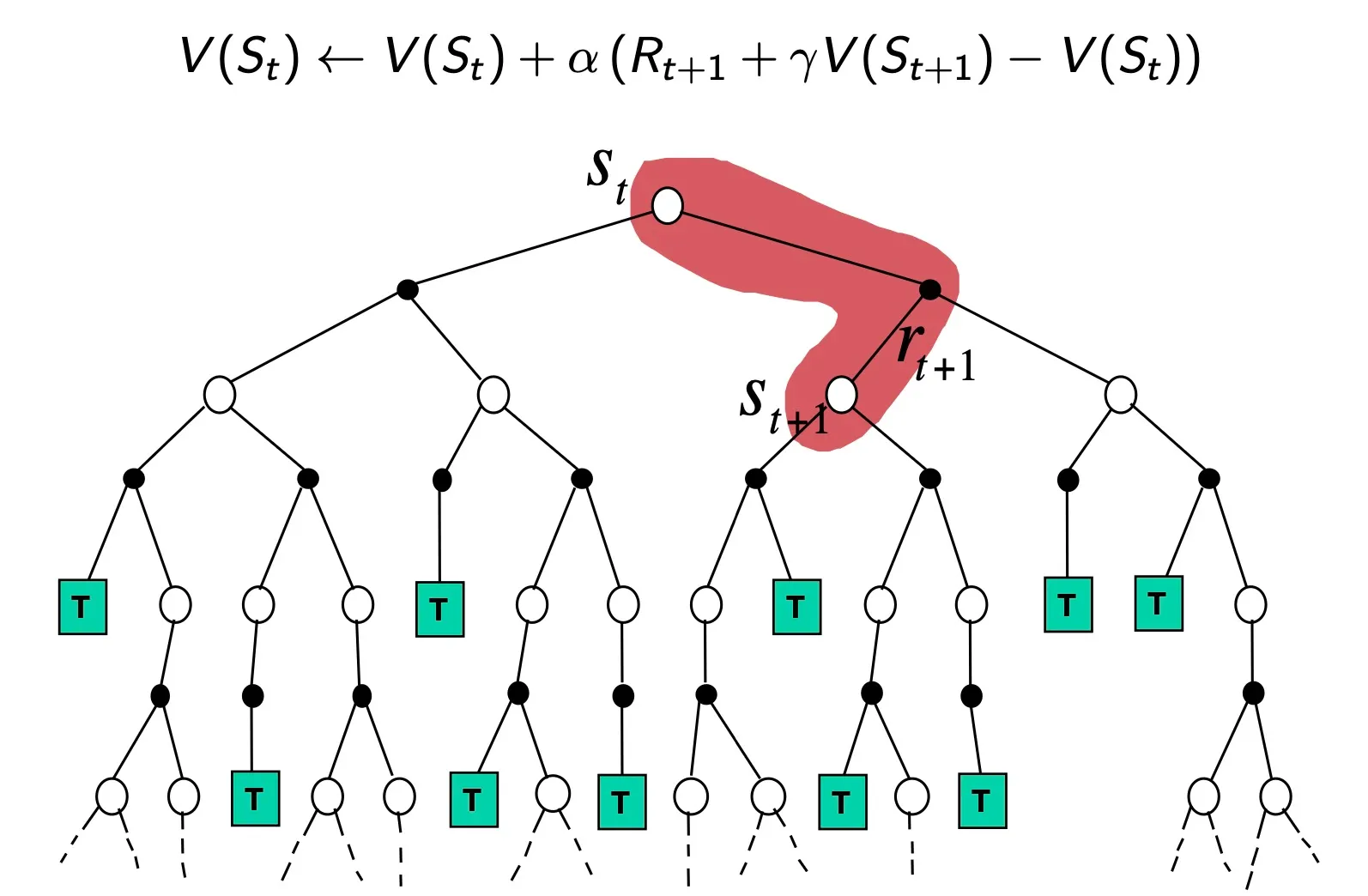
TD Target : Rt+1 + γV (St+1)

→ one-step 더 가서의 예측치

TD error : δt =Rt+1+γV(St+1)−V(St)

→ V(St) : one-step 더 가서의 value 예측치 -V(St+1) : r* one-step에서의 value 예측치

⇒ one-step을 더 가서 예측하는 것이 정확하므로, 그 방향으로 V를 업데이트

MC vs TD

Advantages and Disadvantages of MC , TD

•

MC : final outcome의 return 값이 나온뒤, , complete sequences 에서 학습 가능

terminating 환경에서 사용가능

MC has high variance, zero bias

Good convergence properties (even with function approximation)

Not very sensitive to initial value

Very simple to understand and use

•

TD : final outcome return 값이 나오기 전, incomple sequences 에서 학습 가능

non-terminating 환경에서 사용 가능

TD has low variance, some bias

Usually more efficient than MC

TD(0) converges to vπ(s)

More sensitive to initial value

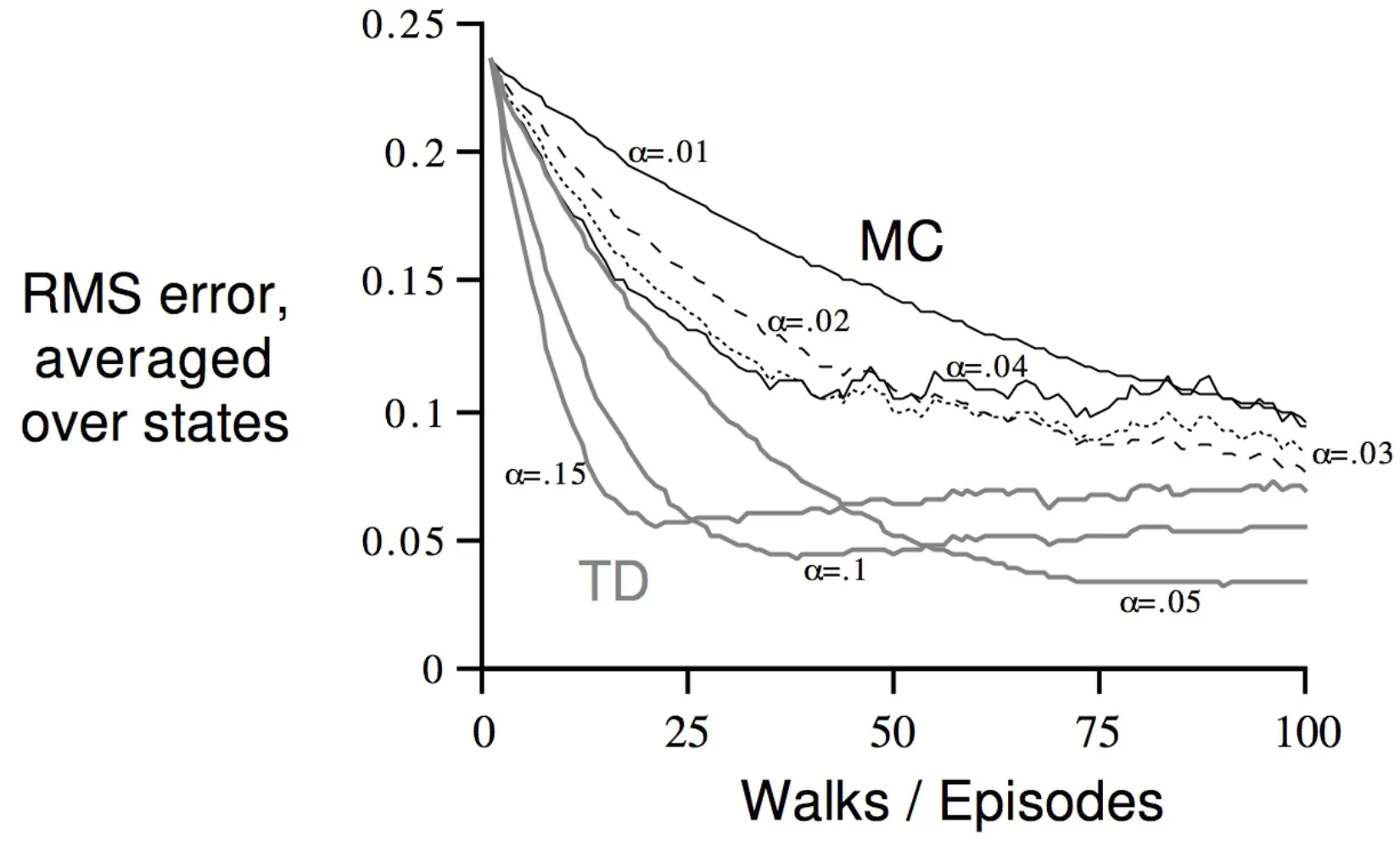
episode가 진행됨에 따라 error가 점점 줄어든다.

MC는 완만히 줄어들고, TD는 a에 따라 진동하는 모습 관찰

Batch MC , TD

episode를 무한번 뽑아낼 수 있으면 MC와 TD가 수렴한다.

MC : Markov property를 사용하지 않고, non-Markov env에서 보통 효과적

TD : Markov property를 사용해서 value를 추측, Markov env에서 더 효과적

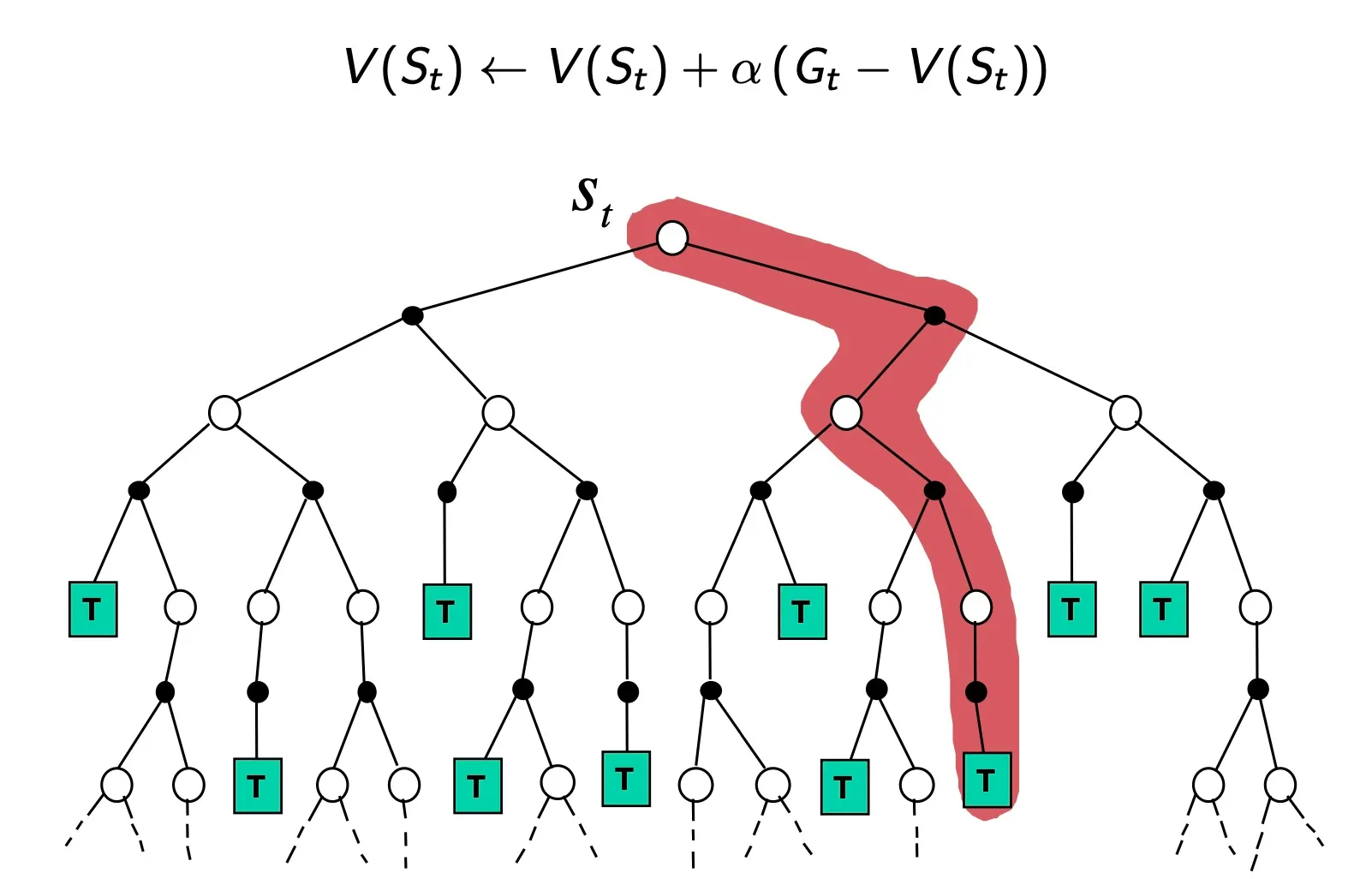
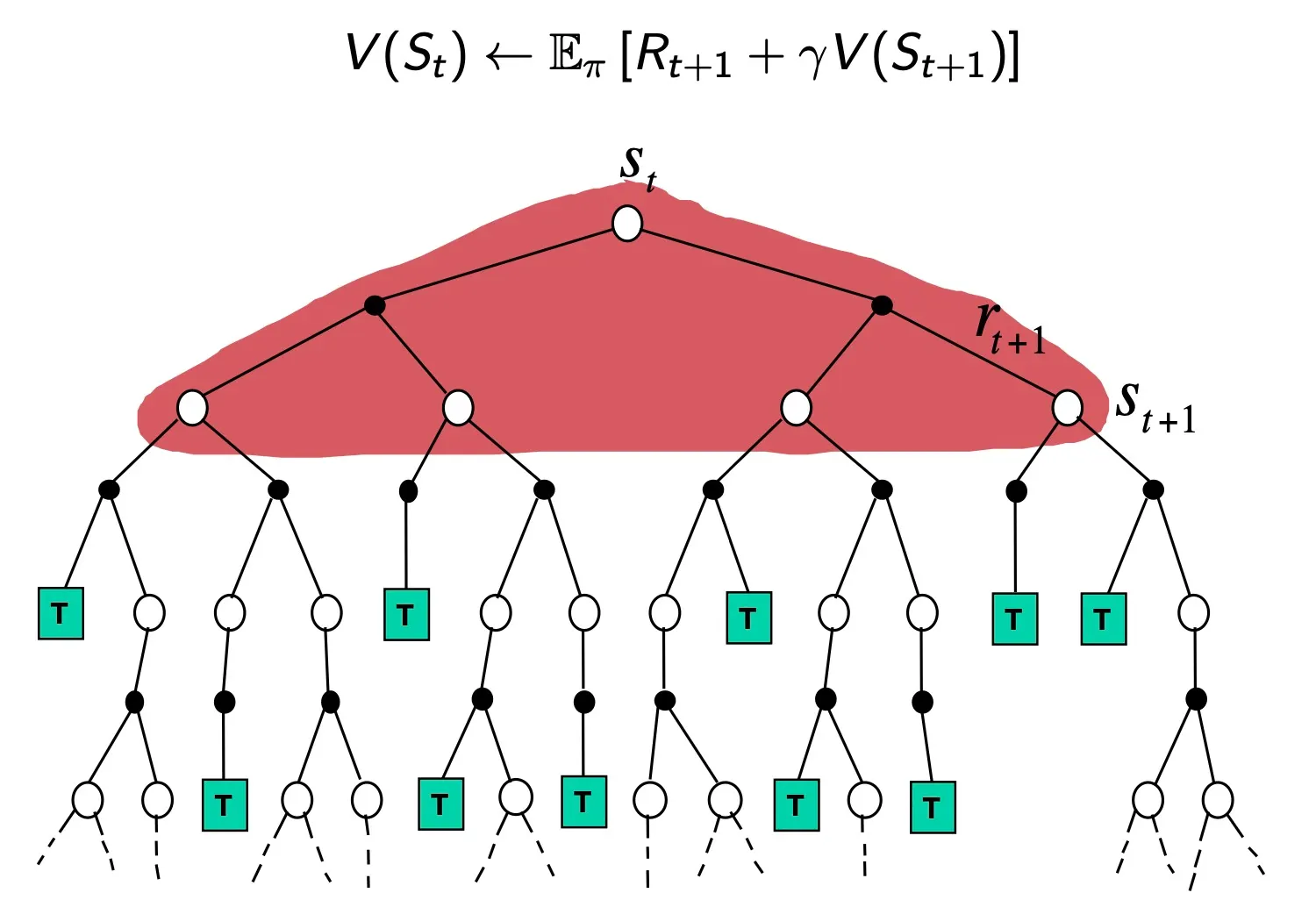
Monte-Carlo Backup

St에서 시작해서 다양한 branches가 존재하는 tree구조

MC는 어느 한가지를 끝까지 해서 이 값으로 St를 update

Temporal-Difference Backup

TD는 한 step만 가보고, 그 상태에서 추측해서 update = bootstrapping

Dynamic Programming Backup

DP는 Sampling 끝까지 해보지 않고, 그 칸에서 할 수 있는 모든 actions에 대해서 한 step 가보고, 그 칸에 적혀 있는 value로 full-width update

Bootstrapping and Sampling

•

Bootstrapping : 추측치로 추측치를 update

MC는 끝까지 가기 때문에 안함, DP와 TD는 한 step만 가서 하기 때문에 적용

•

 한 sample을 통해 update

MC, TD는 Sample을 통해 적용, DP는 그 state에서 적용 가능한 모든 action을 하기 때문에 안함

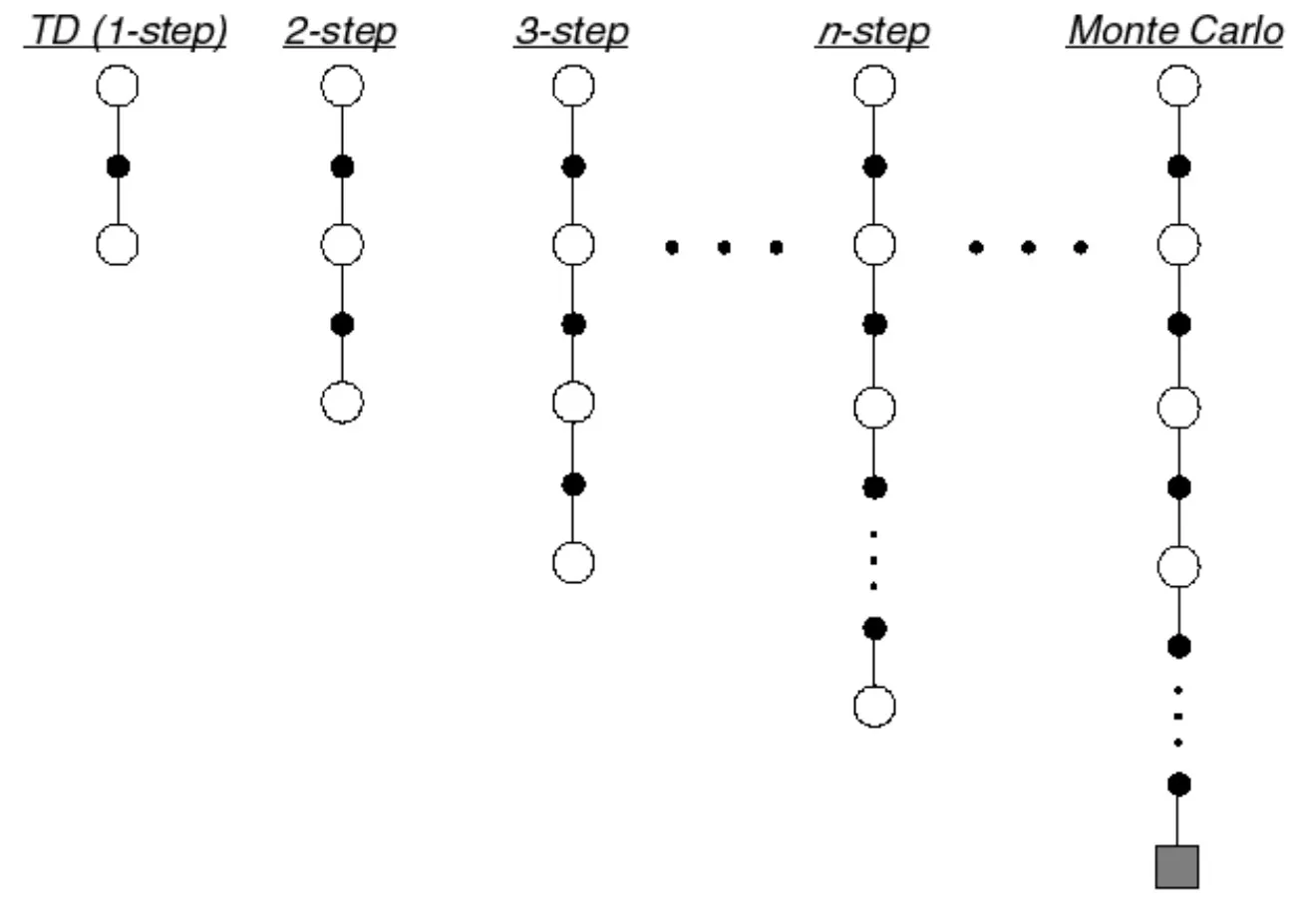
n-Step Prediction

n이 무한대로 가는 TD = MC

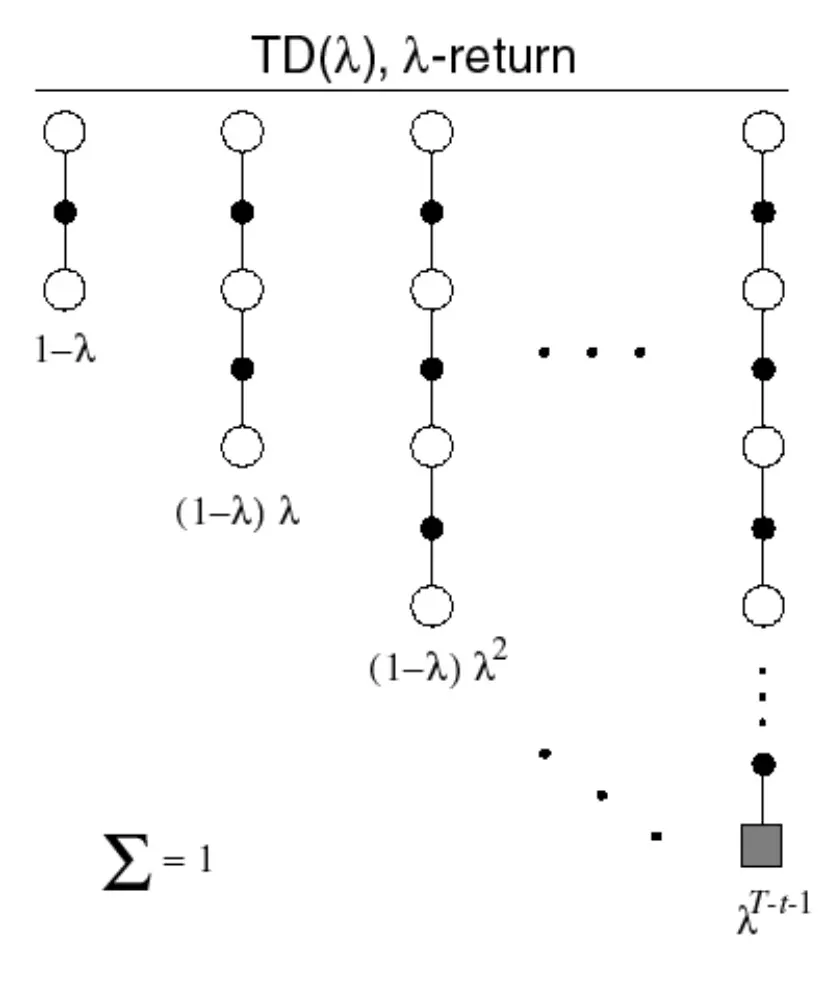
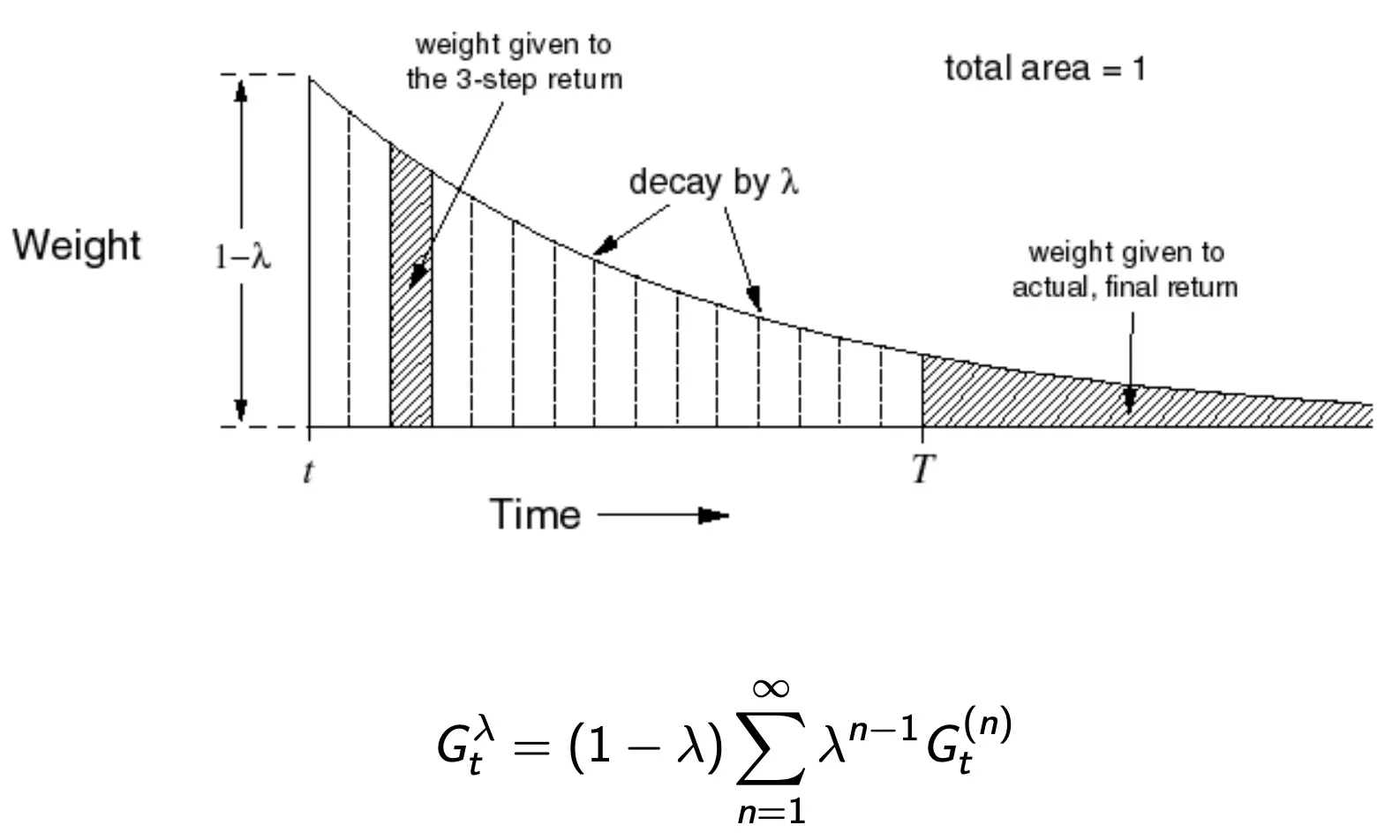
λ-return

TD lamda : TD(0) 부터 MC까지 모든 것을 평균 내도 가능하다.

•

(1 - lamda) 에 lamda를 계속해서 곱해주는 방식, lamda가 곱해지며 MC에 갈수록 가중치가 점점 줄어드는방식

TD(λ) Weighting Function

→ 시간이 지날수록 가중치가 점점 줄어든다.

Geometry means를 사용하면 computation을 efficient하고, memoryless하게 사용할 수 있다.

TD(0)와 같은 비용으로 TD(lamda)를 계산가능하다.

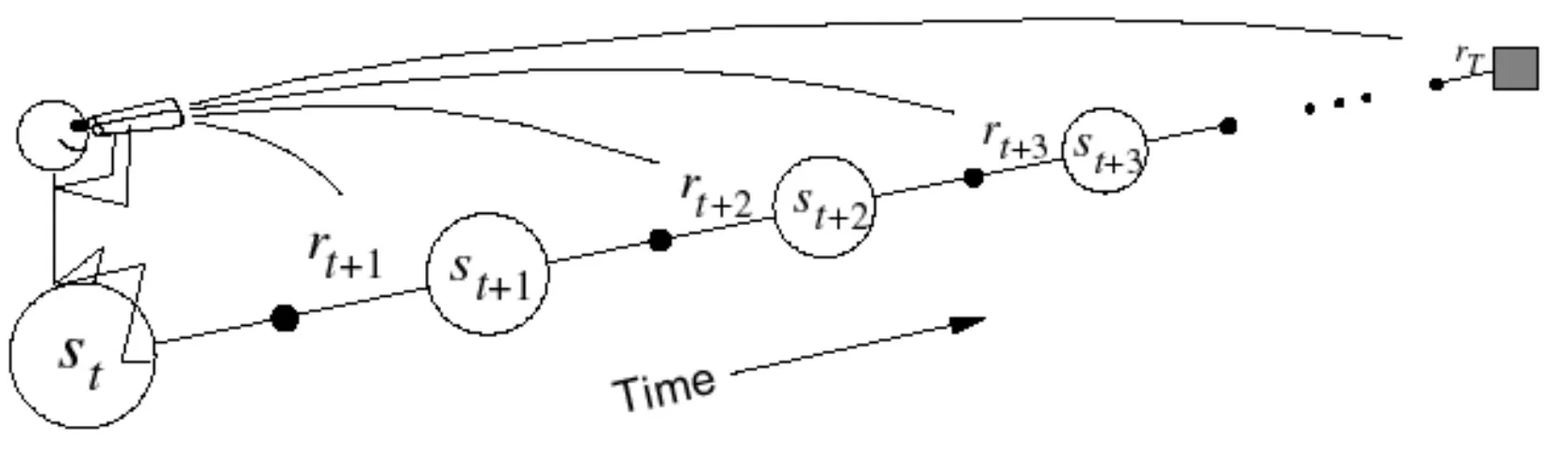
Forward-view TD(lamda)

•

Update value function towards the λ-return

•

Like MC, can only be computed from complete episodes (TD(0)의 장점이 사라짐)

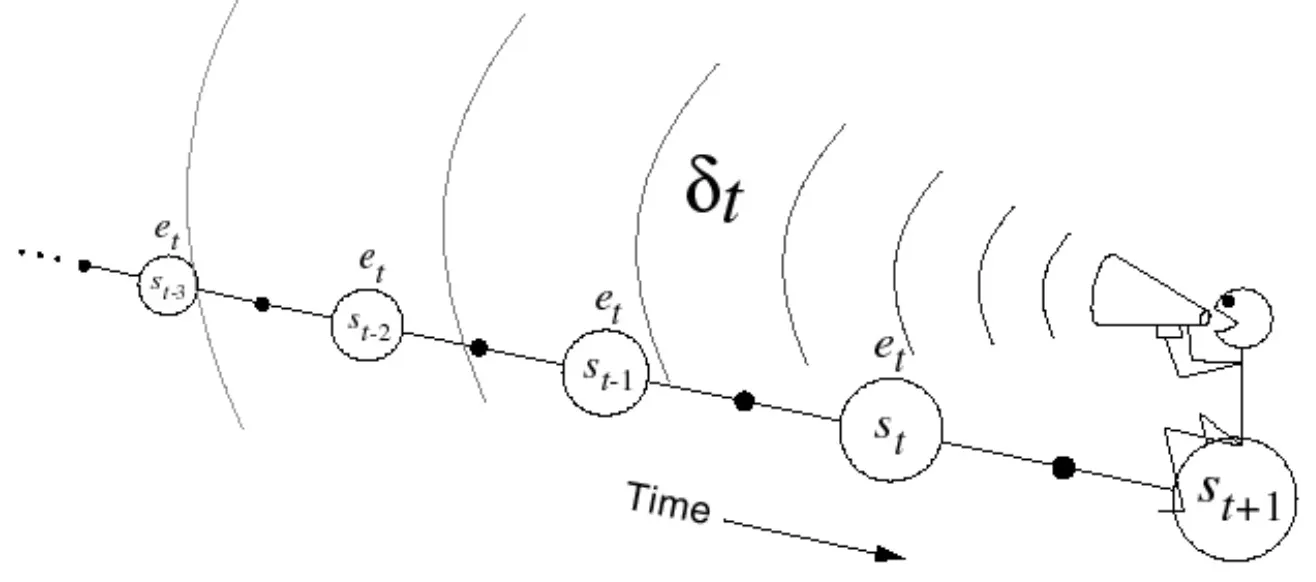
Backward View TD(lamda)

•

Update online, every step, from incomplete sequences (TD(0) 의 장점이 사라짐)

•

Keep an eligibility trace for every state s

•

과거에서 책임소재를 계속 기록하면서 오기 때문에, 매 state마다 update가 가능

대부분의 환경에서 Backward TD(lamda)를 주로 사용

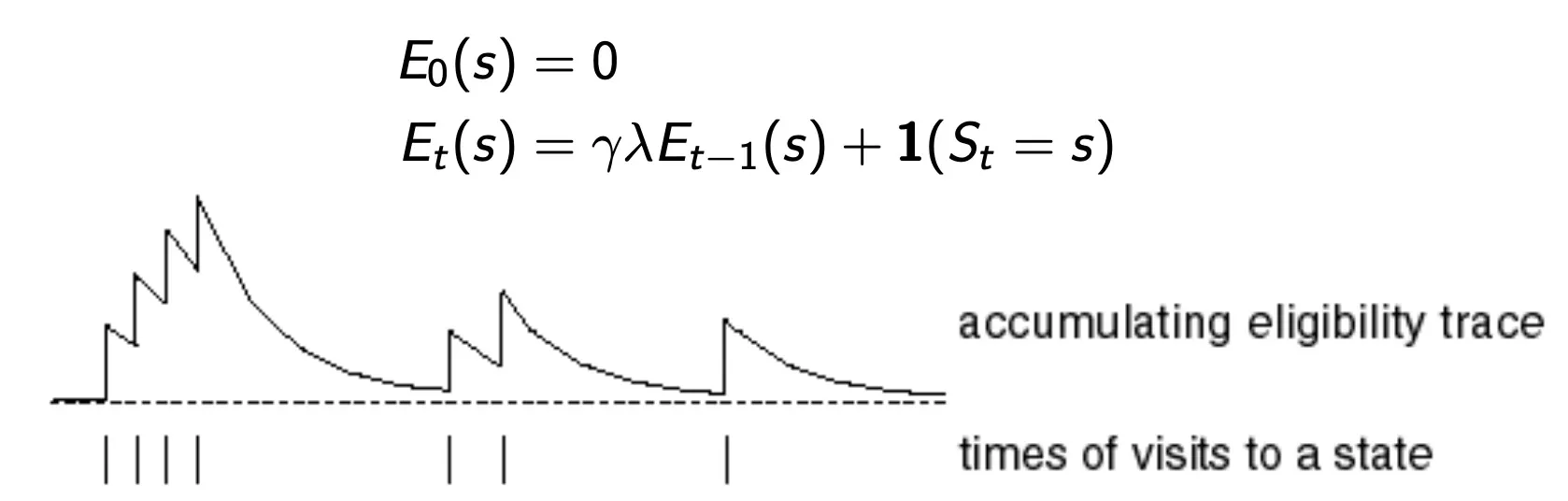
Eligibility Traces

→ 책임이 큰 것한테 update를 많이 해주는 방식

•

Frequency heuristic: assign credit to most frequent states

•

Recency heuristic: assign credit to most recent states

한번도 방문하지 않으면 0, state를 방문하면 1을 더해주고 방문하지 않으면 r곱해서 줄인다.