🦾

DQN

생성일

2024/07/22 02:58

최종 수정일

2025/11/11 02:18

태그

강화학습

작성자

1. Introduction

•

Introduced a CNN architecture to handle high-dimensional image inputs

◦

Enables processing of high-dimensional and continuous state spaces

•

Represents Q-values through a Q-network

◦

Since Q-values must be output for all actions, the action space must be discrete, finite, and of much lower dimensionality compared to the state space

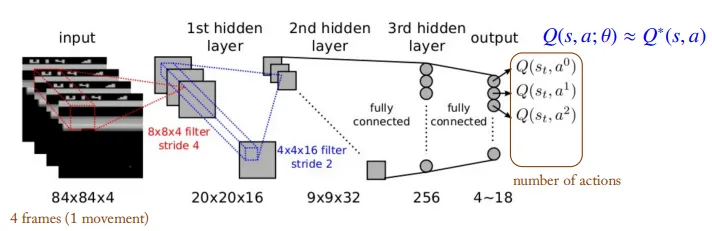
2. DQN Architecture

•

Input

◦

To satisfy the Markov property, four consecutive frames are stacked as the input.

◦

A single frame does not contain sufficient information to predict the future in terms of velocity and direction.

◦

Since the Q-value is computed for a given state input, there are few constraints on the dimensionality of the state space.

•

Convolution Layer

◦

Applies convolution operations to the input images to extract feature vectors and reduce dimensionality.

◦

The last feature maps are flattened so that they can be processed by fully connected layers.

◦

Because spatial information is crucial in games, max pooling—which tends to blur positional details—is not applied.

•

Output

◦

Produces Q-values for each possible action.

◦

The network parameters are updated to ensure that the predicted Q-values approximate the optimal Q-values.

3. Naive DQN

•

Q-learning 

{\small Q(S_t, A_t) ← Q(S_t, A_t) + \alpha [R_{t+1} + \gamma \displaystyle\max_a Q(S_{t+1} ,a ) - Q(S_t, A_t)]}

◦

Target policy:  A greedy policy w.r.t QQQ

◦

Behavior policy: An ϵ−greedy\epsilon - greedyϵ−greedy w.r.t QQQ

◦

The learning process updates the network in a way that minimizes the difference between the Q-value of the current state and its target value.

•

Naive DQN

L(\theta) = [r_{t+1} + \gamma \displaystyle \max_a Q(s_{t+1}, a ; \theta) - Q(s_t, a_t ; \theta)]^2

◦

Define the loss function as the Mean Squared Error

◦

The network is updated by minimizing it

•

Problems

◦

Temporal Correlations

▪

In online RL, parameter updates are executed based on transitions collected over time.

▪

Strong correlations exist between consecutive transitions, which can lead the network to overfit to specific situations.

▪

As a result, the model may fail to sufficiently learn from rare but important experiences.

◦

Non-stationary target

▪

Since the same Q-network is used both to compute the target and to update the Q-values, the target function changes frequently, making convergence difficult.

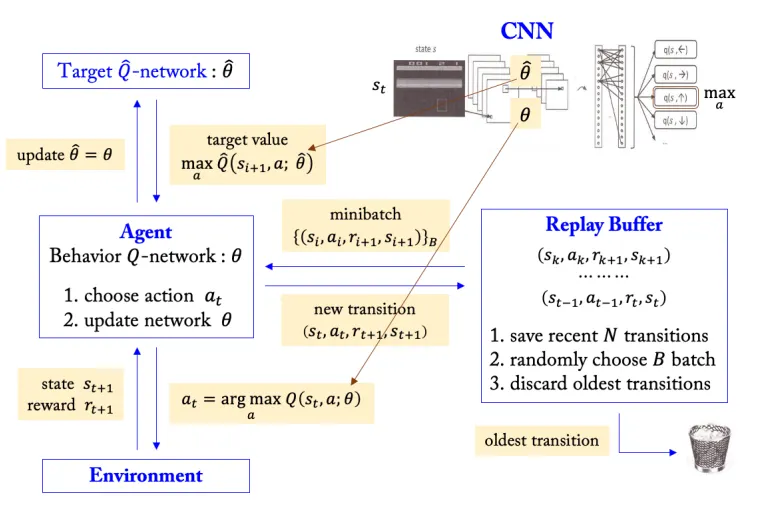
4. Replay buffer

•

Addressing the Temporal Correlation problem

•

Store transitions (s,a,r,s′){(s, a, r, s')}(s,a,r,s′) in replay buffer and randomly sample minibatches from it  for training

•

This reduces temporal correlations between transitions, as each batch can be composed of experiences from different experience and time steps.

•

Improve training efficiency

•

Past experiences can be reused

5. Target Network

•

Initialize the target Q-network parameters θ^\hat{\theta}θ^ to be identical to the behavior Q-network parameters θ\thetaθ at the start of training.

•

During training, θ^\hat{\theta}θ^ fixed while continuously updating θ\thetaθ.

•

After a certain number of steps, update θ^\hat{\theta}θ^ by copying θ\thetaθ.

•

This approach stabilizes training by addressing the problem of a continuously changing target function.

6. DQN

From the current state StS_tSt​, select an action ata_tat​ using the ϵ−greedy\epsilon-greedyϵ−greedy policy based on the behavior network parameters.

Store the transition (st,at,rt+1,st+1)(s_t, a_t, r_{t+1}, s_{t+1})(st​,at​,rt+1​,st+1​) in the replay buffer.

The replay buffer holds the most recent NNN transitions; when a new transition is added, the oldest one is removed.

Randomly sample a minibatch of transitions from the replay buffer.

For the sampled data, compute the target values using the target network parameters.

Compute the loss function L(θ)L(\theta)L(θ).

•

L(θ)=1B∑∣{i=1}∣B[ri+1+γmax⁡aQ^(si+1,a;θ^)−Q(si,ai;θ)]2{\small L(\theta) = \frac{1}{B} \sum_{|\{i=1\}|}^{B} \left[ r_{i+1} + \gamma \max_{a} \hat{Q}(s_{i+1}, a; \hat{\theta}) - Q(s_{i}, a_{i}; \theta) \right]^2}L(θ)=B1​∑∣{i=1}∣B​[ri+1​+γmaxa​Q^​(si+1​,a;θ^)−Q(si​,ai​;θ)]2

•

∇θL(θ)=−1B∑∣{i=1}∣[ri+1+γmax⁡aQ^(si+1,a;θ^)−Q(si,ai;θ)]∇θQ(si,ai;θ){\small \nabla_{\theta} L(\theta) = -\frac{1}{B} \sum_{|\{i=1\}|} \left[ r_{i+1} + \gamma \max_{a} \hat{Q}(s_{i+1}, a; \hat{\theta}) - Q(s_{i}, a_{i}; \theta) \right] \nabla_{\theta} Q(s_{i}, a_{i}; \theta)}∇θ​L(θ)=−B1​∑∣{i=1}∣​[ri+1​+γmaxa​Q^​(si+1​,a;θ^)−Q(si​,ai​;θ)]∇θ​Q(si​,ai​;θ)

Update the behavior network parameters.

After a fixed number of steps, update the target network parameters.

7. Multi-step Learning

Multi-step learning refers to training that uses the n-step return when computing the target values. By choosing an appropriate number of steps, the learning speed can be improved. The loss function used in multi-step learning is defined as follows.

•

  rt+1(n)=∑k=0n−1γkrt+k+1
\; r^{(n)}_{t+1} = \sum_{k=0}^{n-1} \gamma^k r_{t+k+1}
rt+1(n)​=∑k=0n−1​γkrt+k+1​

•

L(θ)=[rt+1(n)+γnmax⁡aQ^(st+n,a;θ^)−Q(st,at;θ)]2{\small L(\theta) =
\Big[ r^{(n)}_{t+1} + \gamma^n \max_a \hat{Q}(s_{t+n}, a; \hat{\theta})-Q(s_t, a_t; \theta) \Big]^2}
L(θ)=[rt+1(n)​+γnmaxa​Q^​(st+n​,a;θ^)−Q(st​,at​;θ)]2