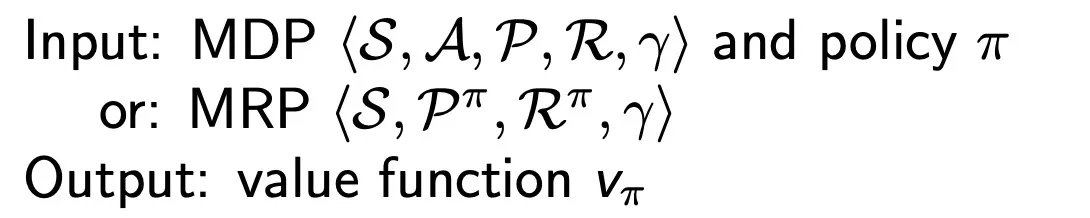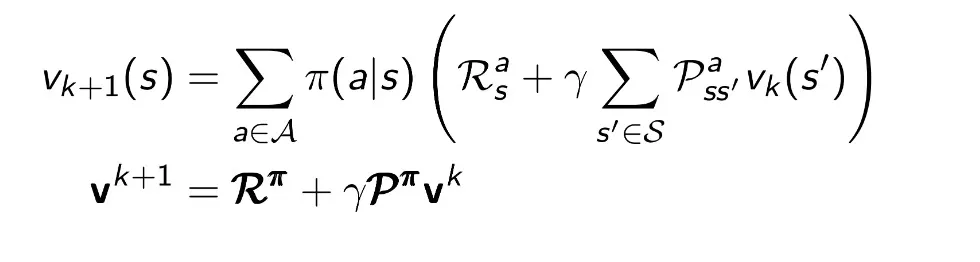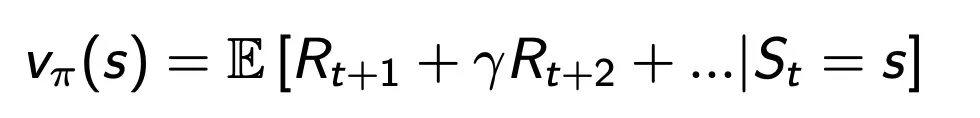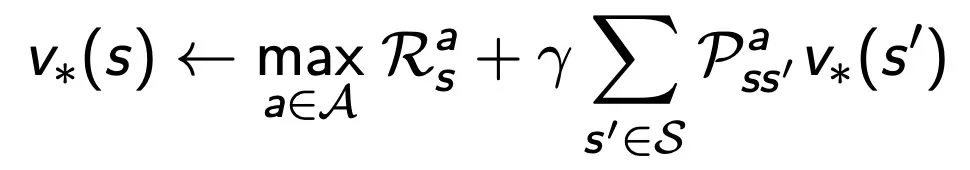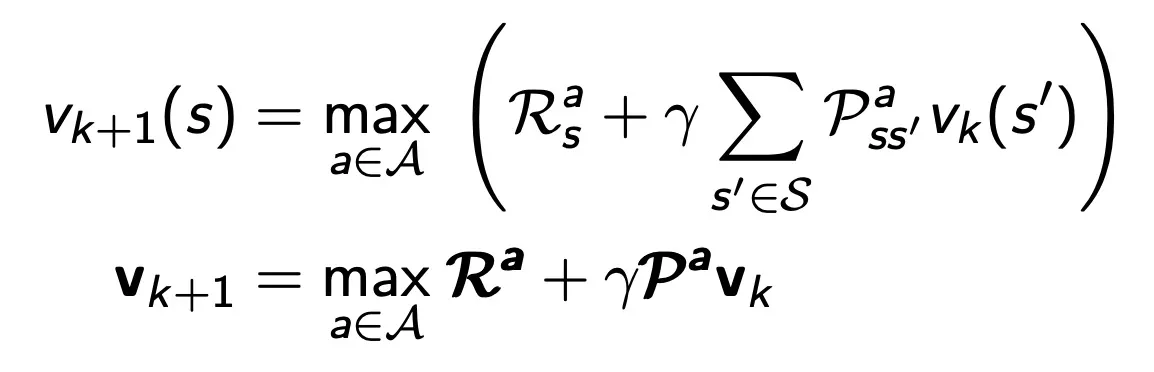🍏

3장

Dynamic Programming

Dynamic : sequential or temporal component to the problem

Programming : optimising a “program” c.f. linear programming

복잡한 문제를 푸는 방법을 의미

Requirements for Dynamic Programming

•

Optimal substructure

•

Overlapping subproblems

DP는 2가지 속성을 가진 문제들을 위한 일반적인 솔루션 방법이다.

Markov decision processes attribute

Bellman equation gives recursive decomposition

Value function stores and reuse solutions

Planning by Dynamic Programming

Planning 이란 모델을 알고 있을 때, MDP를 푸는 문제를 의미한다.

→ 최적의 policy를 찾는 것을 의미

풀다의 의미로 2가지 종류가 있다.

prediction

control

Prediction → value function을 찾는 것

MDP 에서 P는 transition matrix 로써 확률이 담겨 있다.

여기서 policy pi는 optimal 이 아니어도 된다.

어떠한 policy를 던져 주면 그에 맞는 value function을 반환해주는 것을 prediction을 푸는 것이라 한다.

Control → optimal policy를 찾는 것

Policy Evaluation

Iterative Policy Evaluation

Problem : evaluate a given policy pi

Solution : iterative application of Bellman expectation backup

backup은 memory에 저장하게 된다.

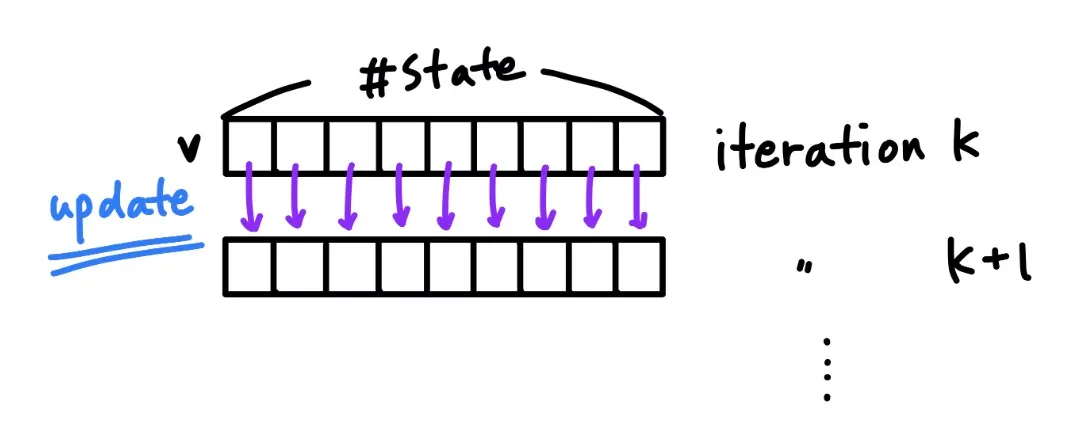
모든 iteration동안에 존재하는 모든 state S에 대해 v(k(s’)) 로부터 v(k+1(s))를 업데이트 하는 것을 synchronous backups라 한다.

s’는 s의 이어지는 state를 의미한다.

위와 같은 계산을 계속하다보면 v(pi)에 수렴한다.

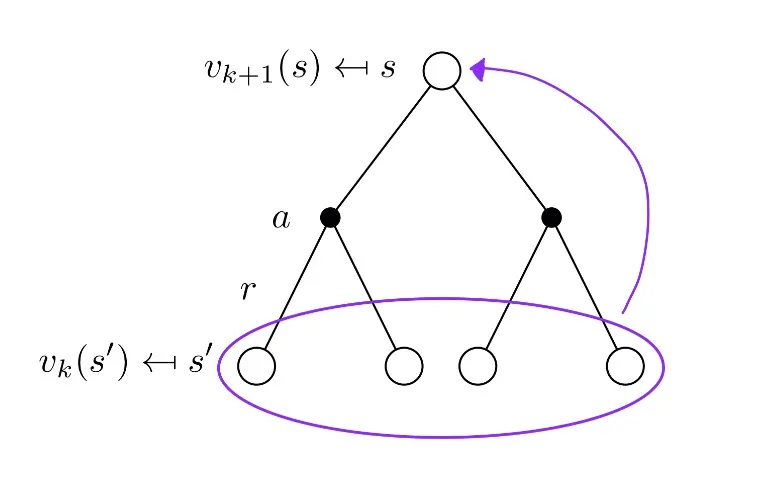
Iterative Policy Evaluation

가장 위에 존재하는 state의 value function은 이전의 state들의 value function 들로 부터 업데이트된다.

Policy Iteration

How to Improve a Policy

Given a policy π

•

Evaluate the policy π

•

Improve the policy by acting greedily with respect to v(π)

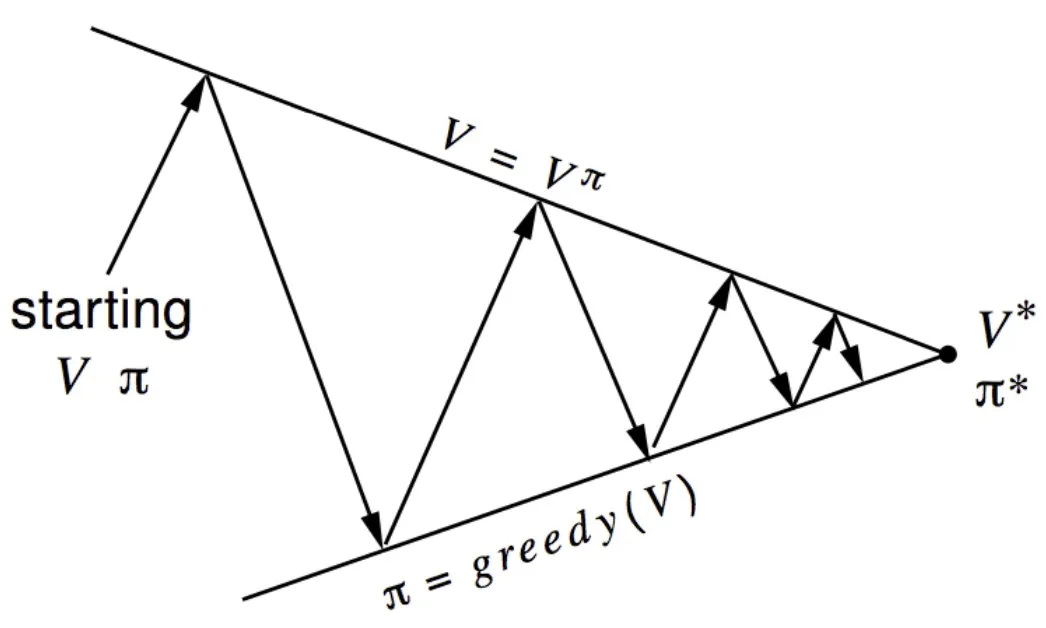
But this process of policy iteration always converges to π∗

시작은 이상해도 끝은 optimal 로 수렴하는 것을 볼 수 있음.

•

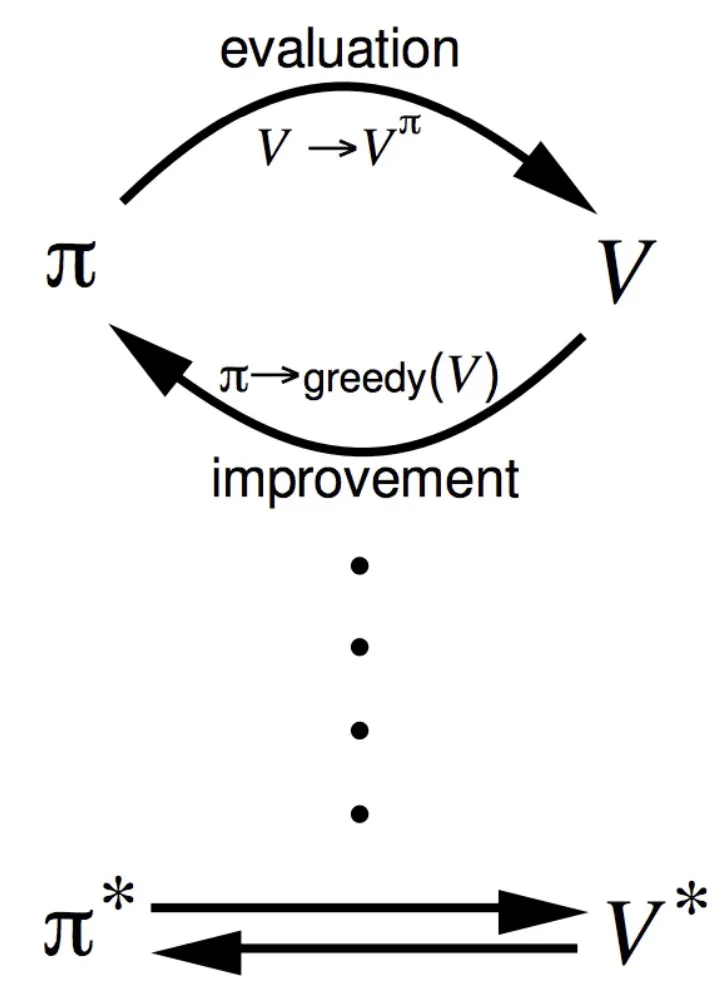
Policy evaluation : Estimate v(π) Iterative policy evaluation

•

Policy improvement : Generate π′ ≥ π Greedy policy improvement

Value Iteration

Principle of Optimality

Any optimal policy can be subdivided into two components:

•

An optimal first action A∗

•

Followed by an optimal policy from successor state S′

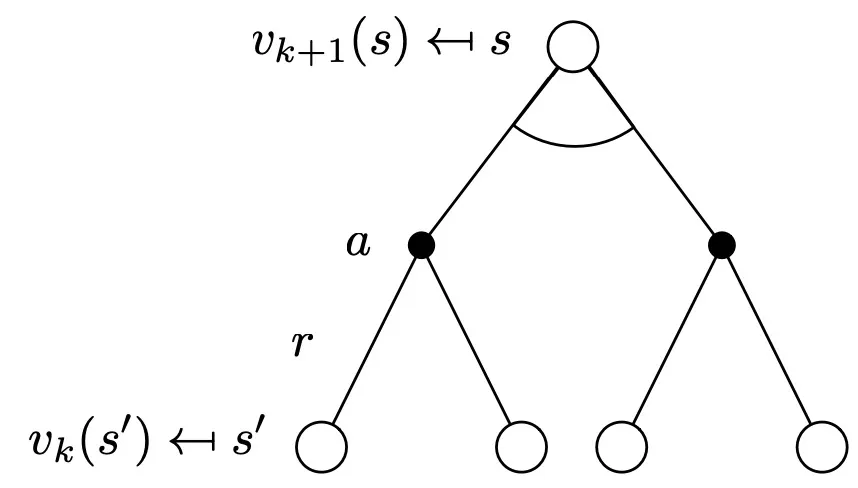
Deterministic Value Iteration

위 식은 nolinear function 때문에 inverse를 구하지 못해 직접적인 솔루션을 계산할 수없어 iterative 방식으로 구해야하는 Optimality Equation 이다.

다음에 갈 수 있는 state에서의 optimal value function을 가지고 현재 state에서의 optimal value를 찾는다는 건 직관적으로 최종 reward로부터 시작해서 거꾸로 앞을 향해 찾아나간다 것을 의미한다.

Value Iteration

•

Unlike policy iteration, there is no explicit policy

•

Intermediate value functions may not correspond to any policy

Synchronous Dynamic Programming Algorithms

Problem	Bellman Equation	Algorithm
Prediction	Bellman Expectation Equation	Iterative Policy Evaluation
Control	Bellman Expectation Equation + Greedy Policy Improvement	policy Iteration
Control	Bellman Optimality Equation	Value Iteration

•

Algorithms are based on state-value function v(π(s)) or v(∗(s))

•

Complexity O(mn2) per iteration, for m actions and n states

Cost가 매우 높음

Asynchronous Dynamic Programming

지금까지의 DP 방식은 synchronous backup 방식을 사용했다.

→ 모든 state들이 parallel 하게 백업이 되었다.

Asynchronous Dynamic Programming 방식은 아무 순서로나 state들을 개별적으로 백업한다.

→ 선택된 각각의 state에 대해서만 적절한 백업을 수행한다.

모든 state들이 골고루 다 뽑힌다면 Convergence를 보장한다.