🦾

Actor-Critic

생성일

2024/08/05 02:59

최종 수정일

2025/11/10 09:34

태그

강화학습

작성자

1. Introduction

•

DQN: Approximates the value function using a neural network.

•

REINFORCE: Approximates the policy using a neural network.

•

Actor-Critic: Utilizes both networks — one for the policy (actor) and one for the value function (critic).

2. Actor-Critic

•

REINFORCE

◦

The policy can only be updated after a full episode has finished

◦

Since the gradient is proportional to the return, it exhibits high variance.

•

Actor-Critic

◦

 By using an estimator instead of GtG_tGt​, the update can be performed without waiting for the episode to finish

▪

That helps alleviate the high variance problem.

◦

Therefore, both the critic network parameterized by ϕ\phiϕ and the actor network parameterized by θ\thetaθ are updated.

•

Gradient(AC)

{\small \nabla_\theta J(\theta)\approx \sum_{t=0}^{T-1} \left( \mathbb{E}_{s_t \sim p_\theta(s_t), a_t \sim \pi_\theta(a_t | s_t)} \left[ \gamma^t \nabla_\theta \log \pi_\theta (a_t | s_t)\ (r(s_t,a_t) + \gamma V_{\pi_\theta}(s_{t+1})-V_{\pi_\theta}(s_t)) \right] \right)}

•

Critic

◦

Evaluate the value of the action selected by the actor.

◦

Update in the direction that improves the accuracy of the value estimation

▪

thus aiming to minimize the MSE between the target and the estimated value.

MC-target:ϕ←ϕ+β(Gt−Vϕ(st))∇ϕVϕ(st)\text{MC-target:} \quad
\phi \leftarrow \phi + \beta \left( G_t - V_{\phi}(s_t) \right) \nabla_{\phi} V_{\phi}(s_t)MC-target:ϕ←ϕ+β(Gt​−Vϕ​(st​))∇ϕ​Vϕ​(st​)

TD-target:ϕ←ϕ+β(rt+1+γVϕ(st+1)−Vϕ(st))∇ϕVϕ(st)\text{TD-target:} \quad
\phi \leftarrow \phi + \beta \left( r_{t+1} + \gamma V_{\phi}(s_{t+1}) - V_{\phi}(s_t) \right)
\nabla_{\phi} V_{\phi}(s_t)TD-target:ϕ←ϕ+β(rt+1​+γVϕ​(st+1​)−Vϕ​(st​))∇ϕ​Vϕ​(st​)

•

Actor

◦

Select an action.

◦

Reflect the critic’s evaluation during the update.

◦

The actor’s objective function is defined with respect to the return, and it is maximized during the update

MC-PG:θ←θ+α(Gt−Vϕ(st))∇θlog⁡πθ(at∣st)\text{MC-PG:} \quad
\theta \leftarrow \theta + \alpha \left( G_t - V_{\phi}(s_t) \right)
\nabla_{\theta} \log \pi_{\theta}(a_t \mid s_t)MC-PG:θ←θ+α(Gt​−Vϕ​(st​))∇θ​logπθ​(at​∣st​)

TD-PG:θ←θ+α(rt+1+γVϕ(st+1)−Vϕ(st))∇θlog⁡πθ(at∣st)\text{TD-PG:} \quad
\theta \leftarrow \theta + \alpha \left( r_{t+1} + \gamma V_{\phi}(s_{t+1})-V_{\phi}(s_t) \right)
\nabla_{\theta} \log \pi_{\theta}(a_t \mid s_t)TD-PG:θ←θ+α(rt+1​+γVϕ​(st+1​)−Vϕ​(st​))∇θ​logπθ​(at​∣st​)

•

Pseudo Code

Select an action in a given state based on the current parameters.

Apply the selected action and observe the reward and next state.

Using the reward and action obtained in step 2, compute the TD-error and update the critic network through gradient descent.

In this step, MSE of the TD-error is used as the objective function for the critic update.

Reflect the result of the TD-error and update the actor network using gradient ascent.

{\small \nabla_\theta J(\theta)\approx \sum_{t=0}^{T-1} \left( \mathbb{E}_{s_t \sim p_\theta(s_t), a_t \sim \pi_\theta(a_t | s_t)} \left[ \nabla_\theta \log \pi_\theta (a_t | s_t)\ (r(s_t,a_t) + \gamma V_{\pi_\theta}(s_{t+1})-V_{\pi_\theta}(s_t)) \right] \right)}

•

in this pseudocode, it proceeds in a 1-step manner where the update is approximated by the sample mean based on the data obtained from each step.

3. A3C

•

A3C is an actor-critic algorithm that utilizes multiple networks.

•

It consists of a global network and multiple worker agents.

◦

Each worker agent learns independently from environment and asynchronously updates the global network.

◦

Since each agent uses a different policy, it naturally promotes exploration.

•

This independence allows each agent to generate diverse experiences at different time steps

◦

Thereby reducing temporal correlation.

•

In addition, when constructing the advantage function in the critic network, A3C uses the n-step return instead of the Q-function

◦

It increases practicality by allowing the critic to operate with only a single parameterized network.

•

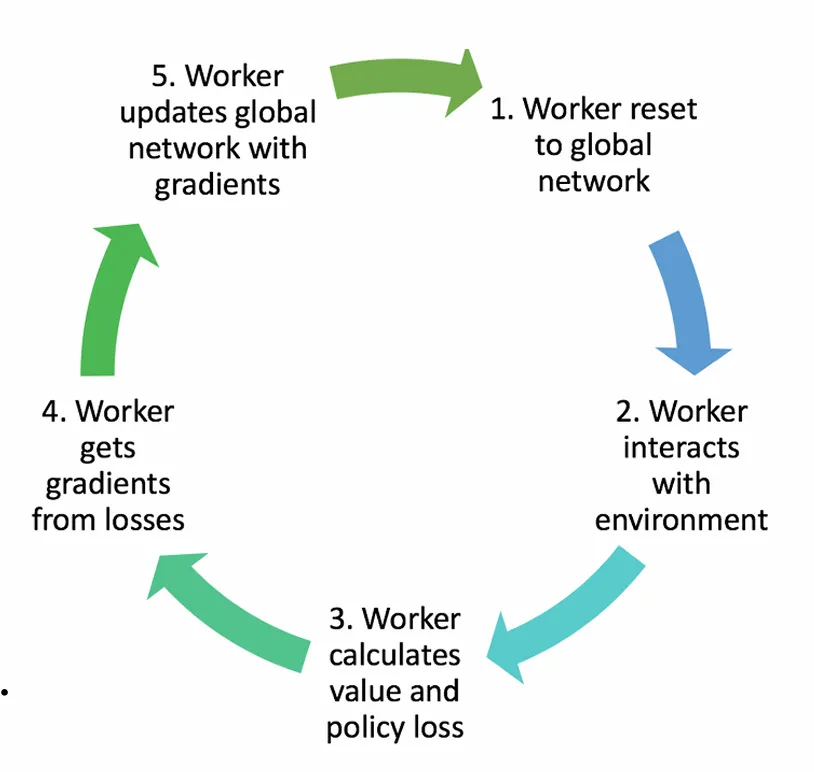
Asynchronous

◦

Initialize each worker agent’s parameters by copying them from the global network.

◦

tmaxmaxtmax_{max}tmaxmax​ steps while computing gradients.

◦

Asynchronously update the global network parameters using the accumulated gradients.

◦

Copy the updated global network parameters for further use.

◦

As a result, the parameters are reset to include updates made by other workers.

•

Advantage

◦

Various forms of the policy gradient consist of two components: one that contains information about the direction in which the parameters should be updated, and another that determines how much the parameters should move in that direction.

◦

In this term, the advantage function can be used in place of the term that indicates the magnitude of update.

◦

Using the advantage function reduces the variance compared to using the return directly.

◦

However, since it requires two parameterized functions (QQQ and VVV), the n-step return is used instead of the Q-function.

◦

As the value of nnn increases, the variance of the advantage estimate increases, whereas a smaller nnn results in lower variance.

◦

n-step Return

G_t ^{(n)} = R_{t+1}+R_{t+2}+ ... + \gamma^n V(s_{n+t})

•

Pseudo Code

Initialize the worker’s network with the parameters of the global network.

tmaxt_{\text{max}}tmax​ steps to obtain a trajectory (worker).

Traverse the time steps in reverse order to compute the n-step return.

Accumulate the gradients for both the actor and critic using the computed n-step returns.

Apply the accumulated gradients to update the global network asynchronously, regardless of whether other agents have finished.